
| n | 1 | 2 | 3 | 4 | �� |
| S | 1 | 3 | 6 | 10 | �� |
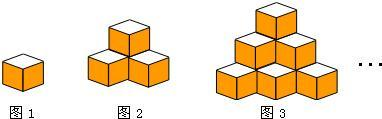
���� ��1����n���С�����εĸ���Ϊǰn�����ĺͣ�
��2�����Ե�9���С�����εĸ���Ϊǰ9�����ĺͣ�Ϊ45��
��3����㼴�ɣ�
��4������κ����Ľ���ʽ��������������з����������ɣ�
���  �⣺��1����һ�㣺S=1��
�⣺��1����һ�㣺S=1��
�ڶ��㣺S=1+2=3��
�����㣺S=1+2+3=6��
���IJ㣺S=1+2+3+4=10��
�ʴ�Ϊ��6��10��
��2����n=9ʱ��S=1+2+3+��+9=45��
�ʴ�Ϊ��45��
��3���ֱ�Ϊ��1��1������2��3������3��6������4��10������ͼ��
��4�������Ƕ��κ����������ʽΪ��S=an2+bn+c��
�ѣ�1��1������2��3������3��6��������������ã�
$\left\{\begin{array}{l}{a+b+c=1}\\{4a+2b+c=3}\\{9a+3b+c=6}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=\frac{1}{2}}\\{c=0}\end{array}\right.$��
��S��n�Ĺ�ϵʽΪ��S=$\frac{1}{2}$${n}^{2}+\frac{1}{2}$n��
���� �����Ƕ��κ�����Ӧ�ã�Ҳ������ƽ��ͼ�εĹ��ɱ仯���⣬ͨ��ѧ������۲�ͼ�Σ����������ɲ���������ɣ���Ӧ��������ɽ�����⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
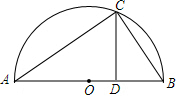 ��ͼ������ABΪֱ���İ�ԲO��һ��C��CD��AB�ڵ�D����֪cos��ACD=$\frac{3}{5}$��BC=6����AC�ij���
��ͼ������ABΪֱ���İ�ԲO��һ��C��CD��AB�ڵ�D����֪cos��ACD=$\frac{3}{5}$��BC=6����AC�ij����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
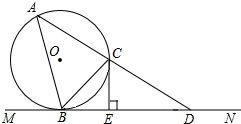 ��ͼ��BC��ԲO���ң�CF��ԲO���ߣ��е�ΪC��������B��MN��CF��E���ҡ�CBM=135�㣬��G��ֱ�߷ֱ���ԲO��MN����A��D���㣮
��ͼ��BC��ԲO���ң�CF��ԲO���ߣ��е�ΪC��������B��MN��CF��E���ҡ�CBM=135�㣬��G��ֱ�߷ֱ���ԲO��MN����A��D���㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ABC�У�AB=BC����ABC=90�㣬FΪAB�ӳ�����һ�㣬��E��BC�ϣ���AE=CF��
��ͼ����ABC�У�AB=BC����ABC=90�㣬FΪAB�ӳ�����һ�㣬��E��BC�ϣ���AE=CF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ���ı���ABCD��ƽ���ı��Σ���E��CD���ϣ�����AE��BD�ڵ�F�������н��۴�����ǣ�������
��ͼ���ı���ABCD��ƽ���ı��Σ���E��CD���ϣ�����AE��BD�ڵ�F�������н��۴�����ǣ�������| A�� | $\frac{AF}{FE}=\frac{BF}{FD}$ | B�� | $\frac{DE}{AB}=\frac{DF}{BD}$ | C�� | $\frac{AF}{AE}=\frac{BF}{BD}$ | D�� | $\frac{DE}{DC}=\frac{EF}{AF}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ƽ��ֱ������ϵ�У�������y=-$\frac{2}{3}$x2+bx+c��x�ύ�ڵ�A��-1��0����B��3��0������y�ύ�ڵ�C��DB��ֱ��x�ᣬCD=CB��M��N�ֱ����߶�BD��BC�ϵĵ㣬�ҡ�CMN=��DBC��
��ͼ����ƽ��ֱ������ϵ�У�������y=-$\frac{2}{3}$x2+bx+c��x�ύ�ڵ�A��-1��0����B��3��0������y�ύ�ڵ�C��DB��ֱ��x�ᣬCD=CB��M��N�ֱ����߶�BD��BC�ϵĵ㣬�ҡ�CMN=��DBC���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com