
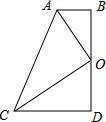
 如图,四边形ABDC中,∠D=∠ABD=90°,点O为BD的中点,且OA平分∠BAC.
如图,四边形ABDC中,∠D=∠ABD=90°,点O为BD的中点,且OA平分∠BAC.分析 (1)过O点作OE⊥AC于点E,利用角平分线的性质定理以及判定定理即可证明.
(2)由Rt△ABO≌Rt△AEO(HL),推出AB=AE,由Rt△CDO≌Rt△CEO(HL),推出CD=CE,推出AB+CD=AE+CE=AC.
解答 证明:(1)过O点作OE⊥AC于点E.
∵∠ABD=90°且OA平分∠BAC
∴OB=OE,
又∵O是BD中点
∴OB=OD,
∴OE=OD,
∵OE⊥AC,∠D=90°
∴点O在∠ACD 的角平分线上
∴OC平分∠ACD.
(2)在Rt△ABO和Rt△AEO中
∵$\left\{\begin{array}{l}OA=OA\\ OB=OE\end{array}\right.$
∴Rt△ABO≌Rt△AEO(HL),
∴AB=AE,
在Rt△CDO和Rt△CEO中
∵$\left\{\begin{array}{l}OC=OC\\ OE=OD\end{array}\right.$
∴Rt△CDO≌Rt△CEO(HL),
∴CD=CE,
∴AB+CD=AE+CE=AC.
点评 本题考查角平分线的性质定理以及判定定理、全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
| A. | x>2 | B. | x≤2且x≠0 | C. | x<2 | D. | x>2且x≠0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x | … | -2 | -1 | 0 | 2 | … |
| y | … | -3 | -4 | -3 | 5 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | -2 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m6÷m2=m3 | B. | 3m3-2m2=m | C. | (3m2)3=27m6 | D. | $\frac{1}{2}$m•2m2=m2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 检测矿区的空气质量 | |
| B. | 审查某篇文章中的错别字 | |
| C. | 调查全国七年级学生视力状况 | |
| D. | 调查山东电视台“我是大明星”的收视率 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com