
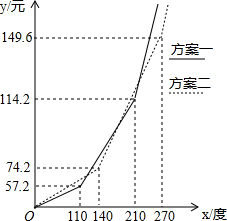
 国家发改委日前表示,居民阶梯电价方案将在今年上半年推出,按发改委先前公布的《居民用电实行阶梯电价的指导意见(征求意见稿)》的标准,绘制了居民每月电费y(元)随本月用电量x(度)变化的图象.根据图象中的有关数据解答下列问题:
国家发改委日前表示,居民阶梯电价方案将在今年上半年推出,按发改委先前公布的《居民用电实行阶梯电价的指导意见(征求意见稿)》的标准,绘制了居民每月电费y(元)随本月用电量x(度)变化的图象.根据图象中的有关数据解答下列问题: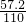 =0.52元;当x≤140时,按方案二,每度电价=
=0.52元;当x≤140时,按方案二,每度电价=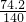 =0.53元;
=0.53元; ,
, ,
, ,
,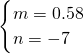 ,
,

 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:初中数学 来源: 题型:
 (2012•南关区模拟)国家发改委日前表示,居民阶梯电价方案将在今年上半年推出,按发改委先前公布的《居民用电实行阶梯电价的指导意见(征求意见稿)》的标准,绘制了居民每月电费y(元)随本月用电量x(度)变化的图象.根据图象中的有关数据解答下列问题:
(2012•南关区模拟)国家发改委日前表示,居民阶梯电价方案将在今年上半年推出,按发改委先前公布的《居民用电实行阶梯电价的指导意见(征求意见稿)》的标准,绘制了居民每月电费y(元)随本月用电量x(度)变化的图象.根据图象中的有关数据解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com