
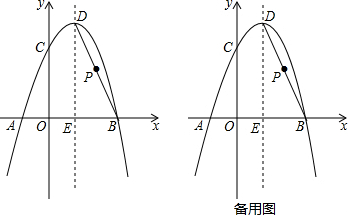
分析 (1)利用待定系数法求出过A,B,C三点的抛物线的函数表达式;
(2)连接PC、PE,利用公式求出顶点D的坐标,利用待定系数法求出直线BD的解析式,设出点P的坐标为(x,-2x+6),利用勾股定理表示出PC2和PE2,根据题意列出方程,解方程求出x的值,计算求出点P的坐标;
(3)设点M的坐标为(a,0),表示出点G的坐标,根据正方形的性质列出方程,解方程即可.
解答 解:(1)∵抛物线y=-x2+bx+c经过A(-1,0),B(3,0)两点,
∴$\left\{\begin{array}{l}{-1-b+c=0}\\{-9+3b+c=0}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{b=2}\\{c=3}\end{array}\right.$,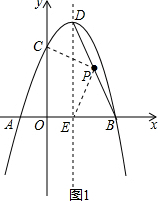
∴经过A,B,C三点的抛物线的函数表达式为y=-x2+2x+3;
(2)如图1,连接PC、PE,
x=-$\frac{b}{2a}$=-$\frac{2}{2×(-1)}$=1,
当x=1时,y=4,
∴点D的坐标为(1,4),
设直线BD的解析式为:y=mx+n,
则$\left\{\begin{array}{l}{m+n=4}\\{3m+n=0}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{m=-2}\\{n=6}\end{array}\right.$,
∴直线BD的解析式为y=-2x+6,
设点P的坐标为(x,-2x+6),
则PC2=x2+(3+2x-6)2,PE2=(x-1)2+(-2x+6)2,
∵PC=PE,
∴x2+(3+2x-6)2=(x-1)2+(-2x+6)2,
解得,x=2,
则y=-2×2+6=2,
∴点P的坐标为(2,2);
(3)设点M的坐标为(a,0),则点G的坐标为(a,-a2+2a+3),
∵以F、M、N、G为顶点的四边形是正方形,
∴FM=MG,即|2-a|=|-a2+2a+3|,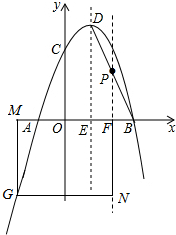
当2-a=-a2+2a+3时,
整理得,a2-3a-1=0,
解得,a=$\frac{3±\sqrt{13}}{2}$,
当2-a=-(-a2+2a+3)时,
整理得,a2-a-5=0,
解得,a=$\frac{1±\sqrt{21}}{2}$,
∴当以F、M、N、G为顶点的四边形是正方形时,点M的坐标为($\frac{3+\sqrt{13}}{2}$,0),($\frac{3-\sqrt{13}}{2}$,0),($\frac{1+\sqrt{21}}{2}$,0),($\frac{1-\sqrt{21}}{2}$,0).
点评 本题考查的是二次函数的图象和性质、待定系数法求函数解析式以及正方形的性质,掌握二次函数的图象和性质、灵活运用待定系数法是解题的关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
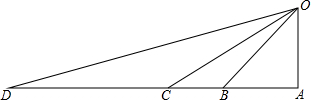 “一号龙卷风”给小岛O造成了较大的破坏,救灾部门迅速组织力量,从仓储D处调集救援物资,计划先用汽车运到与D在同一直线上的C、B、A三个码头中的一处,再用货船运到小岛O.已知:OA⊥AD,∠ODA=15°,∠OCA=30°,∠OBA=45°,CD=20km.若汽车行驶的速度为50km/时,货船航行的速度为25km/时,问这批物资在哪个码头装船,最早运抵小岛O?(在物资搬运能力上每个码头工作效率相同,参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7).
“一号龙卷风”给小岛O造成了较大的破坏,救灾部门迅速组织力量,从仓储D处调集救援物资,计划先用汽车运到与D在同一直线上的C、B、A三个码头中的一处,再用货船运到小岛O.已知:OA⊥AD,∠ODA=15°,∠OCA=30°,∠OBA=45°,CD=20km.若汽车行驶的速度为50km/时,货船航行的速度为25km/时,问这批物资在哪个码头装船,最早运抵小岛O?(在物资搬运能力上每个码头工作效率相同,参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 年龄(岁) | 12 | 13 | 14 | 15 |
| 人数(个) | 2 | 4 | 6 | 8 |
| A. | 13 | B. | 14 | C. | 13.5 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
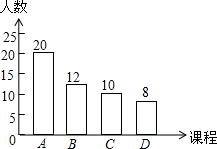 某中学计划开设A、B、C、D四门校本课程供学生选修,规定每个学生必须并且只能选修其中一门,为了了解学生的选修意向,现随机抽取了部分学生进行调查,并将调查结果绘制成如图所示的条形统计图,已知该校学生人数为1200人,由此可以估计选修B课程的学生约有288人.
某中学计划开设A、B、C、D四门校本课程供学生选修,规定每个学生必须并且只能选修其中一门,为了了解学生的选修意向,现随机抽取了部分学生进行调查,并将调查结果绘制成如图所示的条形统计图,已知该校学生人数为1200人,由此可以估计选修B课程的学生约有288人.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com