练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．解方程：
    （1）9-3x=7+5x；
    （2）$\frac{x-0.3}{0.4}$-$\frac{x+0.4}{0.2}$=1．

    分析 （1）方程移项合并，把x系数化为1，即可求出解；
    （2）方程整理后，去分母，去括号，移项合并，把x系数化为1，即可求出解．

    解答 解：（1）移项合并得：8x=2，
    解得：x=0.25；
    （2）方程整理得：$\frac{10x-3}{4}$-$\frac{10x+4}{2}$=1，
    去分母得：10x-3-20x-8=4，
    移项合并得：-10x=15，
    解得：x=-1.5．

    点评 此题考查了解一元一次方程，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    11．若关于x的方程x+$\frac{2}{x}$=c+$\frac{2}{c}$的根为x1=c，x2=$\frac{2}{c}$，则关于x的方程x+$\frac{2}{x-1}$=a+$\frac{2}{a-1}$的根是（　　）
    A．x1=a，x2=$\frac{2}{a-1}$B．x1=a-1，x2=$\frac{2}{a-1}$C．x1=a，x2=$\frac{a+1}{a-1}$D．x1=a，x2=$\frac{a}{a-1}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

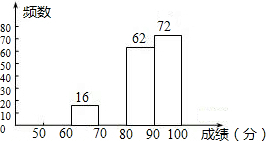    12．某区八年级有3000名学生参加“爱我中华知识竞赛”活动．为了了解本次知识竞赛的成绩分布情况，从中抽取了m名学生的得分进行统计
    成绩x（分）频数频率
    50≤x＜6010a
    60≤x＜70160.08
    70≤x＜80b0.02
    80≤x＜9062c
    90≤x＜100720.36
    请你根据不完整的表格，回答下列问题：
    （1）请直接写出m，a，b，c的值；
    （2）若将得分转化为等级，规定50≤x＜60评为“D”，60≤x＜70评为“C”，70≤x＜90评为“B”，90≤x＜100评为“A”．这次全区八年级参加竞赛的学生约有多少学生参赛成绩被评为“D”？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．无论x取何值，下列不等式总是成立的是（　　）
    A．x+5＞0B．x+5＜0C．-（x+5）2＜0D．（x+5）2≥0

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

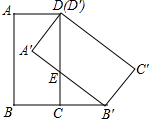    16．如图，在矩形ABCD中，BC=1，将矩形ABCD绕点D逆时针旋转45°，得到矩形A′B′C′D′，点B′恰好落在BC的延长线上，边A′B′交边CD于点E．
    （1）求证：B′C=BC．
    （2）保持矩形A′B′C′D′不动，将矩形ABCD沿射线BB′方向以每秒1个单位的速度平移，设平移时间为t秒．
    ①当矩形ABCD与矩形A′B′C′D′重叠部分为四边形时，求重叠部分的面积为S与t之间的函数关系式．
    ②点A′关于AB的对称点记作点F，直接写出直线DF与矩形A′B′C′D′的边平行时t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．解方程
    （1）7（2y-1）-3（4y-1）-5（3y+2）+1=0；
    （2）$\frac{x+2}{4}$-$\frac{2x-3}{6}$=1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．解方程
    （1）$\frac{3x-1}{2}$=$\frac{4x+2}{5}$-1
    （2）$\frac{3}{2}$[4（x-$\frac{1}{3}$）-$\frac{2}{3}$]=2x．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．如图，在Rt△ABC中，∠ACB=90°，$\frac{BC}{AC}$=$\frac{m}{n}$，CD⊥AB于点D，点E是直线AC上一动点，连接DE，过点D作FD⊥ED，交直线BC于点F．
    （1）探究发现：
    如图1，若m=n，点E在线段AC上，则$\frac{DE}{DF}$=1；
    （2）数学思考：
    ①如图2，若点E在线段AC上，则$\frac{DE}{DF}$=$\frac{n}{m}$（用含m，n的代数式表示）；
    ②当点E在直线AC上运动时，①中的结论是否任然成立？请仅就图3的情形给出证明；
    （3）拓展应用：若AC=$\sqrt{5}$，BC=2$\sqrt{5}$，DF=4$\sqrt{2}$，请直接写出CE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．在三角形ABC中，∠BAC=90°，AB=AC．
    （1）如图1，点D是CA延长线上一点，点E在线段AB上，且AD=AE，连接BD和CE，延长CE交BD于点F，连接AF．求证：BD=CE；
    （2）在（1）得条件下，求∠AFD的度数；
    （3）如图2，点P是△ABC外一点，∠APB=45°，猜想PA、PB、PC三条线段长度之间存在的等量关系，并证明你的结论．

    查看答案和解析>>

    同步练习册答案