
【题目】已知m2﹣mn=2,mn﹣n2=5,则3m2+2mn﹣5n2= .
【答案】31
【解析】解:方法一: 根据题意,m2﹣mn=2,mn﹣n2=5,故有m2=2+mn,n2=mn﹣5,
∴原式=3(2+mm)+2mn﹣5(mn﹣5)=31.
故应填31.
方法二:根据已知条件m2﹣mn=2,mn﹣n2=5,得
m(m﹣n)=2,n(m﹣n)=5
∴两式相加得,(m+n)(m﹣n)=7,m+n= ![]()
∴3m2+2mn﹣5n2=3(m+n)(m﹣n)+2n(m﹣n)
=3( ![]() )(m﹣n)+2(
)(m﹣n)+2( ![]() )(m﹣n)
)(m﹣n)
=21+10
=31.
故应填31.
【考点精析】关于本题考查的代数式求值和因式分解的应用,需要了解求代数式的值,一般是先将代数式化简,然后再将字母的取值代入;求代数式的值,有时求不出其字母的值,需要利用技巧,“整体”代入;因式分解是整式乘法的逆向变形,可以应用与数字计算、求值、整除性问题、判断三角形的形状、解方程才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】对非负实数 ![]() “四舍五入”到个位的值记为
“四舍五入”到个位的值记为 ![]() . 即当n为非负整数时,若
. 即当n为非负整数时,若 ![]() ,则
,则 ![]() =
= ![]() . 如:
. 如: ![]() =3,
=3, ![]() =4,…根据以上材料,解决下列问题:
=4,…根据以上材料,解决下列问题:
(1)填空 ![]() = ,
= , ![]() =;
=;
(2)若 ![]() ,则
,则 ![]() 的取值范围是;
的取值范围是;
(3)求满足 ![]() 的所有非负实数
的所有非负实数 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,∠A=60°,AB=12cm,若点P从点B出发以2cm/s的速度向点A运动,点Q从点A出发以1cm/s的速度向点C运动,设P、Q分别从点B、A同时出发,运动的时间为ts. 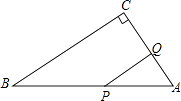
(1)用含t的式子表示线段AP、AQ的长;
(2)当t为何值时,△APQ是以PQ为底边的等腰三角形?
(3)当t为何值时,PQ∥BC?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区为了绿化环境,计划分两次购进A,B两种花草,第一次分别购进A,B两种花草30棵和15棵,共花费675元;第二次分别购进A,B两种花草12棵和5棵.两次共花费940元(两次购进的A,B两种花草价格均分别相同).
(1)A,B两种花草每棵的价格分别是多少元?
(2)若购买A,B两种花草共31棵,且B种花草的数量少于A种花草的数量的2倍,请你给出一种费用最省的方案,并求出该方案所需费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com