

���� ��1����k=1ʱ��������������ֱ�ߵĽ���ʽ���ⷽ����õ�A��B�����ꣻ
��2���籸��ͼ1���������ߣ������ABM����ı���ʽ��Ȼ�����ö��κ���������������ֵ����M�����ꣻ
��3��������Ψһһ��N��ʹ��ON��DN���ĺ����ǣ���ODΪֱ����Բ��ֱ��AB�����ڵ�N����Բ�ܽǶ�����֪����ʱ��OND=90���ҵ�NΪΨһ���Դ�Ϊ�������������������Σ����ñ���ʽ�г����̣����k��ֵ��
��� �⣺��1����k=1ʱ�������߽���ʽΪy=-x2+1��ֱ�߽���ʽΪy=x-1��
������������ʽ���ã�-x2+1=x-1��
��ã�x=-2��x=1��
��x=-2ʱ��y=x-1=-3����x=1ʱ��y=x-1=0��
��A��-2��-3����B��1��0����
��2����M��x��-x2+1����
�籸��ͼ1��ʾ������M��MP��y�ᣬ��ֱ��AB�ڵ�P����P��x��x-1����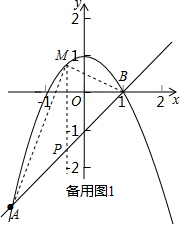
��PM=yM-yP=��-x2+1��-��x-1��=-x2-x+2��
S��ABM=S��PMA+S��PMB=$\frac{1}{2}$PM��xM-xA��+$\frac{1}{2}$PM��xB-xM��=$\frac{1}{2}$PM��xB-xA��=$\frac{3}{2}$PM��
��S��ABM=$\frac{3}{2}$��-x2-x+2��=-$\frac{3}{2}$��x+$\frac{1}{2}$��2+$\frac{27}{8}$��
��x=-$\frac{1}{2}$ʱ��yM=-x2+1=$\frac{3}{4}$��
���ABM������ֵΪ$\frac{27}{8}$����ʱ��M����Ϊ��-$\frac{1}{2}$��$\frac{3}{4}$����
��3����ֱ��AB��y=kx-1��x�ᡢy��ֱ��ڵ�E��F��
��E��$\frac{1}{k}$��0����F��0��-1����OE=$\frac{1}{k}$��OF=1��
��Rt��EOF�У��ɹ��ɶ����ã�EF=$\sqrt{��\frac{1}{k}��^{2}+1}$=$\frac{\sqrt{1+{k}^{2}}}{k}$��
��y=-x2+��k-1��x+k=0������-x+k����x+1��=0����ã�x=k��x=-1��
��D��k��0����OD=k��
����Ψһһ��N��ʹ��ON��DN���籸��ͼ2��ʾ��
����ODΪֱ����Բ��ֱ��AB�����ڵ�N������Բ�ܽǶ�������ʱ��OND=90�㣮
���SΪOC�е㣬����NS����NS��EF��NS=DS=OS=$\frac{k}{2}$��
��ES=OE-OS=$\frac{1}{k}$-$\frac{k}{2}$��
�ߡ�NES=��FEO����ENS=��EOF=90�㣬
���ENS�ס�EOF��
��$\frac{NS}{OF}$=$\frac{ES}{EF}$������$\frac{\frac{k}{2}}{1}$=$\frac{\frac{1}{k}-\frac{k}{2}}{\frac{\sqrt{1+{k}^{2}}}{k}}$��
��ã�k=��$\frac{2\sqrt{5}}{5}$��
��k��0��
��k=$\frac{2\sqrt{5}}{5}$��
�����Ψһһ��N��ʹ��ON��DN����ʱk=$\frac{2\sqrt{5}}{5}$��
���� �����Ƕ��κ���ѹ���⣬�ۺϿ����˶��κ�����һ�κ�����ͼ�������ʡ��ⷽ�̡����ɶ�����ֱ����Բ��λ�ù�ϵ�����Ƶ���Ҫ֪ʶ�㣬��һ�����Ѷȣ��ڣ�2�����У�ע��ͼ������ļ��㷽�����ڣ�3�����У�����ؼ������⡰����Ψһһ��N��ʹ��ON��DN���ĺ��壮


 ��һ������Ԫͬ�����ؾ�ϵ�д�
��һ������Ԫͬ�����ؾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
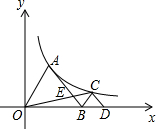 ��ͼ���ȱߡ�OAB��ȱߡ�BCD�ı�OB��BD��x���������ϣ���A�͵�C��˫����y=$\frac{k}{x}$��x��0���ϣ�����OC��AB�ڵ�E����$\frac{CE}{OE}$=$\sqrt{2}$-1��
��ͼ���ȱߡ�OAB��ȱߡ�BCD�ı�OB��BD��x���������ϣ���A�͵�C��˫����y=$\frac{k}{x}$��x��0���ϣ�����OC��AB�ڵ�E����$\frac{CE}{OE}$=$\sqrt{2}$-1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��OCƽ�֡�AOB��DΪOC��һ�㣬DE��OB��E����DE=5����D��OA�ľ���Ϊ5��
��ͼ��OCƽ�֡�AOB��DΪOC��һ�㣬DE��OB��E����DE=5����D��OA�ľ���Ϊ5���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��AD�ǵȱߡ�ABC�����ߣ�AE=AD�����EDC�Ķ���Ϊ��������
��ͼ��AD�ǵȱߡ�ABC�����ߣ�AE=AD�����EDC�Ķ���Ϊ��������| A�� | 30�� | B�� | 20�� | C�� | 25�� | D�� | 15�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com