
【题目】为开展阳光体育活动,某班需要购买一批羽毛球拍和羽毛球,现了解情况如下:甲、乙两家商店岀售同样品牌的羽毛球拍和羽毛球,羽毛球拍毎副定价30元,羽毛球每盒定价5元,且两家都有优惠:甲店每买一副球拍赠一盒羽毛球;乙店全部按定价的9折优惠.
(1)若该班需购买羽毛球拍5副,购买羽毛球![]() 盒(不小于5盒).当购买多少盒羽毛球时,在两家商店购买所花的钱相等?
盒(不小于5盒).当购买多少盒羽毛球时,在两家商店购买所花的钱相等?
(2)若需购买10副羽毛球拍,30盒羽毛球,怎样购买更省钱?
【答案】(1)当购买羽毛球20盒时,两种优惠办法付款一样;(2)最省钱的方案为:到甲店购买10副球拍,得到10副球拍,10盒球,再到乙店购买20盒羽毛球,需费用390元.
【解析】
(1)设当购买羽毛球x盒时,两种优惠办法付款一样,根据甲、乙两店的优惠方式,分别用x表示出两店的费用,再根据甲店的费用等于乙店的费用列出方程解答即可;
(2)分别计算出①全部在甲店购买所需费用,②全部在乙店购买所需费用,③到甲店购买10副球拍,得到10副球拍,10盒球,再到乙店购买20盒羽毛球所需费用,进行对比可得出最省方案.
(1)设当购买羽毛球x盒时,两种优惠办法付款一样,可得:
甲店:![]() 元,
元,
乙店:![]() 元;
元;
依题意得:![]()
解得:![]() ,
,
答:当购买羽毛球20盒时,两种优惠办法付款一样.
(2)①若全部在甲店购买,则费用为![]() (元),
(元),
②若全部在乙店购买,则费用为![]() (元)
(元)
③若到甲店购买10副球拍,得到10副球拍,10盒球,再到乙店购买20盒羽毛球,
则费用为![]() (元).
(元).
所以最省钱的方案为:到甲店购买10副球拍,得到10副球拍,10盒球,再到乙店购买20盒羽毛球,需费用390元.


 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
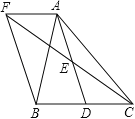
(1)BD与CD有什么数量关系,并说明理由;
(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
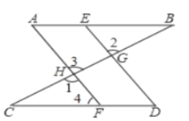
【题目】已知:如图,点![]() 分别是
分别是![]() 上的点,
上的点,![]() 分别交
分别交![]() 于
于![]() ,试说明
,试说明![]() .阅读下面的解题过程,在横线上补全推理过程或依据.
.阅读下面的解题过程,在横线上补全推理过程或依据.
解:![]() (已知)
(已知)
![]() (______________________)
(______________________)
![]() (等量代换)
(等量代换)
![]() (_____________________)
(_____________________)
∴![]() (__________________________)
(__________________________)
又![]() (已知)
(已知)
![]() (等量代换)
(等量代换)
![]() ______(____________________________)
______(____________________________)
![]() (_________________________)
(_________________________)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一劳动节大酬宾!”,某商场设计的促销活动如下:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“50元”的字样.规定:在本商场同一日内,顾客每消费满300元,就可以在箱子里先后摸出两个球(第一次摸出后不放回).商场根据两小球所标金额的和返还相等价格的购物券,购物券可以在本商场消费.某顾客刚好消费300元.
(1)该顾客至多可得到元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于50元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若x满足(x-4) (x-9)=6,求(x-4)2+(x-9)2的值.
解:设x-4=a,x-9=b,则(x-4)(x-9)=ab=6,a-b=(x-4)-(x-9)=5,
∴(x-4)2+(x-9)2=a2+b2=(a-b)2+2ab=52+2×6=37
请仿照上面的方法求解下面问题:
(1)若x满足(x-2)(x-5)=10,求(x-2)2 + (x-5)2的值
(2)已知正方形ABCD的边长为x,E,F分别是AD、DC上的点,且AE=1,CF=3,长方形EMFD的面积是15,分别以MF、DF作正方形,求阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某翼装飞行员从离水平地面高AC=500m的A处出发,沿着俯角为15°的方向,直线滑行1600米到达D点,然后打开降落伞以75°的俯角降落到地面上的B点.求他飞行的水平距离BC(结果精确到1m).
查看答案和解析>>
科目:初中数学 来源: 题型:
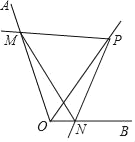
【题目】如图,点P为定角∠AOB的平分线上的一个定点,点M,N分别在射线OA,OB上(都不与点O重合),且∠MPN与∠AOB互补.若∠MPN绕着点P转动,那么以下四个结论:①PM=PN恒成立;②MN的长不变;③OM+ON的值不变;④四边形PMON的面积不变.其中正确的为_____.(填番号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据调查,超速行驶是引发交通事故的主要原因之一,所以规定以下情境中的速度不得超过15m/s,在一条笔直公路BD的上方A处有一探测仪.如图,AD=24m,∠D=90°,第一次探测到一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°
(1)求B,C的距离.
(2)通过计算,判断此轿车是否超速.(tan31°≈0.6,tan50°≈1.2,结果精确到1m)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中(AB≠BC),直线EF经过其对角线的交点O,且分别交AD,BC于点M,N,交BA,DC的延长线于点E,F,下列结论:①AO=BO;②OE=OF;③△EAM≌△FCN;④△EAO≌△DCO.其中一定正确的是()
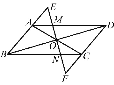
A. ①② B. ②③
C. ①④ D. ①③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com