
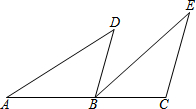
 已知:如图,点A、B、C在一条直线上,BD∥CE,AB=EC,BD=CB.
已知:如图,点A、B、C在一条直线上,BD∥CE,AB=EC,BD=CB. 提分百分百检测卷系列答案
提分百分百检测卷系列答案科目:初中数学 来源: 题型:解答题
 如图,已知AD∥BC,∠D=∠DAE,
如图,已知AD∥BC,∠D=∠DAE,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB,CD是两根钉在木板上的平行木条,将一根橡皮筋固定在A,C两点,点E是橡皮筋上的一点,拽动E点将橡皮筋拉紧后,请你探索∠A,∠AEC,∠C之间具有怎样的关系并说明理由.(提示:先画出示意图,再说明理由).
如图,AB,CD是两根钉在木板上的平行木条,将一根橡皮筋固定在A,C两点,点E是橡皮筋上的一点,拽动E点将橡皮筋拉紧后,请你探索∠A,∠AEC,∠C之间具有怎样的关系并说明理由.(提示:先画出示意图,再说明理由).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,∠BAC=90°,AD⊥BC于点D,△ABE、△ACF都是等边三角形,求证:
如图,△ABC中,∠BAC=90°,AD⊥BC于点D,△ABE、△ACF都是等边三角形,求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 填空:把下面的推理过程补充完整,并在括号内注明理由.
填空:把下面的推理过程补充完整,并在括号内注明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com