
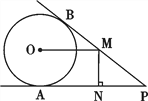
【题目】如图,PA,PB分别与⊙O相切于点A,B,点M在PB上,且OM∥AP,MN⊥AP,垂足为N.
(1)求证:OM = AN;
(2)若⊙O的半径R = 3,PA = 9,求OM的长.
【答案】(1)证明见解析;(2)5.
【解析】试题分析:(1)连接OA,由切线的性质可知OA⊥AP,再由MN⊥AP可知四边形ANMO是矩形,故可得出结论;
(2)连接OB,则OB⊥BP由OA=MN,OA=OB,OM∥AP.可知OB=MN,∠OMB=∠NPM.故可得出Rt△OBM≌△MNP,OM=MP.设OM=x,则NP=9-x,在Rt△MNP利用勾股定理即可求出x的值,进而得出结论.
试题解析:(1)如图,连接OA,则OA⊥AP,

∵MN⊥AP,
∴MN∥OA,
∵OM∥AP,
∴四边形ANMO是矩形,
∴OM=AN;
(2)解:连接OB,则OB⊥BP
∵OA=MN,OA=OB,OM∥AP.
∴OB=MN,∠OMB=∠NPM.
∴Rt△OBM≌Rt△MNP,
∴OM=MP.
设OM=x,则NP=9-x,
在Rt△MNP中,有x2=32+(9-x)2
∴x=5,即OM=5.


科目:初中数学 来源: 题型:
【题目】货主两次租用某汽车运输公司的甲,乙两种货车运送货物往某地,第一次租用甲货车2辆和乙货车3辆共运送15.5吨货物,第二次租用甲货车3辆和乙货车2辆共运送17吨货物,两次运输都按货车的最大核定载货量刚好将货物运送完,没有超载.
(1)求甲,乙两种货车每辆最大核定载货量是多少吨?
(2)已知租用甲种货车运费为每辆1200元,租用乙种货车运费为每辆800元,现在货主有24吨货物需要运送,而汽车运输公司只有2辆甲种货车,其它的都是乙种货车,问有几种租车方案?哪种方案费用较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是我们生活中经常接触的小刀,刀片的外壳是四边形,而且刀片外壳与刀片铆合部分都是直角,刀片的上、下是平行的,转动刀片时会形成∠1和∠2,则∠1+∠2的度数为( )

A. 80° B. 70° C. 90° D. 100°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种衬衣原价168元,连续两次降价a%后售价为128元.下面所列方程中正确的是( )
A. 168(1+a%)2=128 B. 168(1-a%)2=128
C. 168(1-2a%)=128 D. 168(1-a2%)=128
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连接AE,F为AE上一点,且∠BFE=∠C.
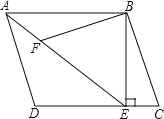
(1)求证:△ABF∽△EAD;
(2)若AD=3,∠BAE=30°,求BF的长.(计算结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线交于点O,点O又是正方形A1B1C1O的一个顶点,而且这两个正方形的边长相等、无论正方形A1B1C1O绕点O怎样转动,两个正方形重叠部分的面积,总等于一个正方形面积的

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com