Question

在凸五边形ABCDE中，S_△ABC=S_△BCD=S_△CDE=S_△DEA=S_△EAB=1，CE与AD相交于F，求S_△CFD．

Answer 1

分析：根据等底的两个三角形，若面积相等，则高相等，易得AD∥BC、CE∥AB、BD∥AE、BE∥CD、AC∥DE；设S_△AEF=x，S_△DEF=1-x，即AF：DF=x：（1-x）．由△DEF与△CAF相似，根据他们的面积比等于相似比的平方列方程求解．

解答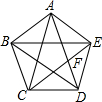：解：∵S_△BCD=S_△CDE，
∴BE∥CD．
同理可得AD∥BC、CE∥AB、BD∥AE、AC∥DE．
∴四边形ABCF是平行四边形．
∴三角形ACF和三角形ABC的面积相等，都是1．
设S_△AEF=x，则S_△DEF=1-x，即AF：DF=x：（1-x），
∵△DEF∽△ACF，
∴x²：（1-x）²=1：（1-x），
解得x=

5 -1

2

．
∴S_三角形CFD=1-（1-x）=x=

5 -1

2

．

点评：本题综合性较强，有一定的难度，考查了平行四边形的判定与性质，相似三角形的判定与性质．解题关键是等底的两个三角形，若面积相等，可得高相等，及由面积比等于相似比的平方列出方程．