
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源:2016~2017学年安徽省芜湖市九年级下学期第一次模拟考试数学试卷(解析版) 题型:单选题
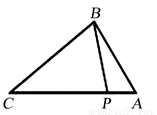
如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是( )
A. 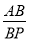 =
= B. ∠APB=∠ABC C.
B. ∠APB=∠ABC C. 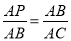 D. ∠ABP=∠C
D. ∠ABP=∠C
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
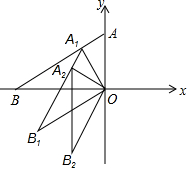 如图,点A(0,1),点B(-$\sqrt{3}$,0),作OA1⊥AB,垂足为A1,以OA1为边作Rt△A1OB1,使∠A1OB1=90°,∠B1=30°,作OA2⊥A1B1,垂足为A2,再以OA2为边作Rt△A2OB2,使∠A2OB2=90°,∠B2=30°,…,以同样的作法可得到Rt△AnOBn,则当n=2017时,点A2017的纵坐标为( )
如图,点A(0,1),点B(-$\sqrt{3}$,0),作OA1⊥AB,垂足为A1,以OA1为边作Rt△A1OB1,使∠A1OB1=90°,∠B1=30°,作OA2⊥A1B1,垂足为A2,再以OA2为边作Rt△A2OB2,使∠A2OB2=90°,∠B2=30°,…,以同样的作法可得到Rt△AnOBn,则当n=2017时,点A2017的纵坐标为( )| A. | ($\frac{\sqrt{3}}{2}$)2017 | B. | -($\frac{\sqrt{3}}{2}$)2017 | C. | ($\frac{\sqrt{3}}{2}$)2018 | D. | -($\frac{\sqrt{3}}{2}$)2018 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
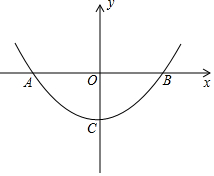 抛物线y=ax2+c与x轴交于A、B两点,顶点为C,点P在抛物线上,P(1,-3),B(4,0).
抛物线y=ax2+c与x轴交于A、B两点,顶点为C,点P在抛物线上,P(1,-3),B(4,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
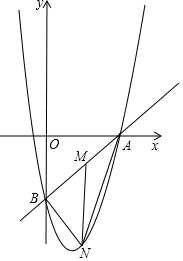 如图,直线y=$\frac{3}{4}$x-3与x轴、y轴交于A,B两点,抛物线y=x2+bx+c经过点A,B两点,M是射线BA上一个动点,MN∥y轴交抛物线于点N.
如图,直线y=$\frac{3}{4}$x-3与x轴、y轴交于A,B两点,抛物线y=x2+bx+c经过点A,B两点,M是射线BA上一个动点,MN∥y轴交抛物线于点N.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
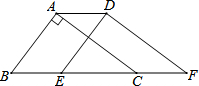 如图,在Rt△ABC中,∠BAC=90°,∠ACB=30°,AB=2,将△ABC沿直线BC向右平移得到△DEF,连接AD,若AD=2,则点C到DF的距离为( )
如图,在Rt△ABC中,∠BAC=90°,∠ACB=30°,AB=2,将△ABC沿直线BC向右平移得到△DEF,连接AD,若AD=2,则点C到DF的距离为( )| A. | 1 | B. | 2 | C. | 2.5 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
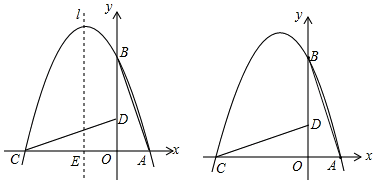
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com