
Ϊ����Ӧ���ҡ�������ҵ���ĺ��٣�ij��ѧ��ҵ��������һ��װ��Ʒ�̵꣬�ɹ���һ�ֽ�������е���Ʒ������30��������������۸�Ϊ20Ԫ/�������۽�����֪��������P������������ʱ��x���죩֮��Ĺ�ϵ��ͼ��1����ʾ�����ۼ۸�Q��Ԫ/����������ʱ��x���죩֮��Ĺ�ϵ��ͼ��2����ʾ��
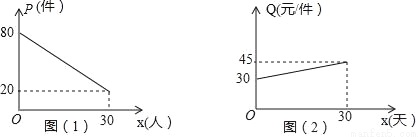
��1������ͼ��ֱ��д������������P������������ʱ��x���죩֮��ĺ�����ϵʽΪ�� �������۵���
Q��Ԫ/����������ʱ��x���죩�ĺ�����ϵʽΪ�� ��������Ҫ��д���Ա�����ȡֵ��Χ��
��2��д������Ʒ������������W��Ԫ��������ʱ��x���죩֮��ĺ�����ϵʽ������Ҫ��д���Ա�����ȡֵ��Χ��
��3��������30����������У���һ�����������������������������
��1��P=��2x+80��Q=x+30����2��W=��x2+20x+800����3����30��������У���10�����������������������Ϊ900Ԫ �������������������1����P��kx��80������30��20����������k��ֵ���ó���������P������������ʱ��x���죩֮��ĺ�����ϵʽ����Q��mx��30������30��45����������m��ֵ���ó�Q��Ԫ/����������ʱ��x���죩�ĺ�����ϵʽ�� ��2��������...
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2018�˽̰���꼶��ѧ�²���ϰ����ʮ���´����� ���ͣ������
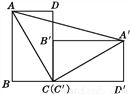
��ͼ������ֱ���õij�����ש��ABCD�Ƶ���������A'B'C'D'��λ�ã�������ABCD�ij��Ϳ��ֱ�Ϊa��b��AC�ij�Ϊc.
��1��������ֻ��a��b�Ĵ���ʽ��ʾS��ABC��S��C'A'D'��Sֱ������A'D'BA��?����ֻ��c�Ĵ���ʽ��ʾS��ACA'��?
��2������(1)�Ľ��ۣ�������֤���ɶ�����?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�����Ϻӿ���2018����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ���ѡ��
����O��һ��M����ҳ�Ϊ10cm������ҳ�Ϊ8cm����ôOM��Ϊ�� ��
A. 3cm B. 6cm C. 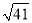 cm D. 9cm
cm D. 9cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�걱ʦ������꼶��ѧ�ϲ��5�� һԪһ�η��� ��Ԫ���Ծ� ���ͣ���ѡ��
һԪһ�η���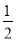 x��1��2�Ľ��ʾ�������ϣ���ͼ�������ϵ��ĸ���(����)
x��1��2�Ľ��ʾ�������ϣ���ͼ�������ϵ��ĸ���(����)
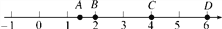
A. D�� B. C�� C. B�� D. A��
A ���������������� ����ȥ��ĸ�ã�x��2=4����ã�x=6���ѷ��̵Ľ��ʾ�������ϣ���ͼ�������ϵ�D�㣬��ѡA���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�걱ʦ������꼶��ѧ�ϲ��5�� һԪһ�η��� ��Ԫ���Ծ� ���ͣ���ѡ��
С����������ҵ����С�Ľ������е�һ��������Ⱦ�ˣ�����Ⱦ�ķ�����2��x��3��������x��1����ô���أ���������㷭�����Ĵ𰸣����̵Ľ���x��9�������������Ⱦ�ij����ǣ�������
A. 1 B. 2 C. 3 D. 4
B ���������������� �豻��Ⱦ������Ϊy�� ��x=9����ã�2��6��y=10�� ��ã�y=2�� ��ѡB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ������Т����2016-2017ѧ����꼶���ϣ���ĩ������ѧ�Ծ� ���ͣ������
�������
��1��2x2��4x=12
��2��4x��2x+1��=6x+3��
(1)x=1����2��x=����x= �������������������1�����䷽�������� �������߳���2�Ѷ�����ϵ����Ϊ1��Ȼ��������һ����ϵ��һ���ƽ����ʹ���Ϊ��ȫƽ��ʽ���ұ��dz����Ȼ��ֱ�ӿ�ƽ����⼴�ɣ� ��2���ѷ����ұߵ����������ʽ3��������ߣ��������������ʽ(2x��1)��ʹ����ת��Ϊ������ʽ�Ļ�����0����ʽ��Ȼ��ת��Ϊ����һԪһ�η�����⼴�ɣ� ��������� ����...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ������Т����2016-2017ѧ����꼶���ϣ���ĩ������ѧ�Ծ� ���ͣ���ѡ��
��ͼ���������ABCDE�ڽ��ڡ�O������A��������CB���ӳ����ཻ�ڵ�F�����F=�� ��
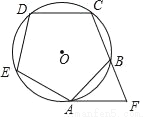
A. 18�� B. 36�� C. 54�� D. 72��
D ���������������������OA��OB�� ��AF�ǡ�O�����ߣ� ���OAF��90�㣬 ���������ABCDE�ڽ��ڡ�O�� ���AOB����72�㣬 ��OA��OB�� ���OAB����OBA����54�㣬 ���BAF��90�㣭54�㣽36�㣬 �ߡ�ABF����72�㣬 ���F��180�㣭36�㣭72�㣽72�㣬 ��ѡD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�������ʡ�����жŶ������ؾ��꼶���ϣ���ĩ��ѧ�Ծ�������ѧ�ƣ� ���ͣ������
 ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ���ݵ���2017-2018ѧ��ȵ�һѧ����ĩ�����꼶��ѧ�Ծ� ���ͣ������
��֪��MAN=120�㣬��C�ǡ�MAN��ƽ����AQ�ϵ�һ�����㣬��B��D�ֱ���AN��AM�ϣ�����BD��
�����֡�
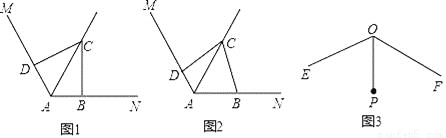
��1����ͼ1������ABC=��ADC=90�㣬���BCD=�� ���㣬��CBD���� �������Σ�
��̽����
��2����ͼ2������ABC+��ADC=180�㣬���жϡ�CBD����״����֤����Ľ��ۣ�
��Ӧ�á�
��3����ͼ3����֪��EOF=120�㣬OPƽ�֡�EOF����OP=1������G��H�ֱ�������OE��OF�ϣ��ҡ�PGHΪ�ȱ������Σ����������������ġ�PGH�ĸ���һ������ ������ֻ����ţ�
��2�� ��3�� ��4�� ��4������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com