
已知:如图,正比例函数y=ax的图象与反比例函数y=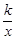 的图象交于点A(3,2).
的图象交于点A(3,2).
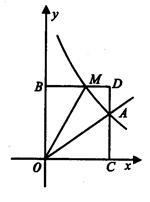
(1)确定上述正比例函数和反比例函数的表达式
(2)根据图象回答,在第一象限内,当x取何值时,反比例函数的值大于正比例函数的值?
(3)M(m,n)是反比例函数图象上的一个动点,其中0<m<3,过点M作直线MB//x轴,交y轴于点B;过点A作直线AC//y轴交x轴于点C,交直线MB于点D.当四边形OADM的面积为3时,请判断线段BM与DM有何数量关系,并说明理由.
(1)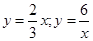 (2)
(2)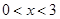 (3)BM=2DM
(3)BM=2DM
【解析】
试题分析:(1)将A(3,2)分别代入y= kx,y=ax中,得ak的值,进而可得正比例函数和反比例函数的表达式;
(2)观察图象,得在第一象限内,当0<x<3时,反比例函数的图象在正比例函数的上方;故反比例函数的值大于正比例函数的值;
(3)有S△OMB=S△OAC= 12×|k|=3,可得S矩形OBDC为12;即OC?OB=12;进而可得m n的值,故可得BM与DM的大小;比较可得其大小关系.
解答:解:(1)将A(3,2)分别代入y=" k" x,y=ax中,得:2= k3,3a=2
∴k=6,a= 23
∴反比例函数的表达式为:y= 6x
正比例函数的表达式为y= 23x
(2)观察图象,得在第一象限内,当0<x<3时,反比例函数的值大于正比例函数的值.
(3)BM=DM
理由:∵S△OMB=S△OA= 12×|k|=3
∴S矩形OBDC=S四边形OADM+S△OMB+S△OAC=3+3+6=12
即OC?OB=12
∵OC=3
∴OB=4
即n=4
∴m= 6n=32
∴MB= 32,MD="3-" 32= 32
∴MB=MD
考点:函数的几何意义以及与不等式组之间的联系
点评:该题较为复杂,结合了正比例函数、一次函数与不等式组之间的关系,以及与几何意义,是常考的知识点。


 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:初中数学 来源: 题型:
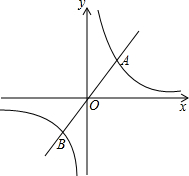 如图,已知正比例函数y=x与反比例函数y=
如图,已知正比例函数y=x与反比例函数y=| 1 | x |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| x |
| 1 |
| x |
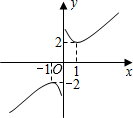 象似双钩,我们称之为“双钩函数”).给出下列几个命题:
象似双钩,我们称之为“双钩函数”).给出下列几个命题:查看答案和解析>>
科目:初中数学 来源: 题型:
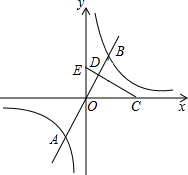 如图,已知正比例函数y=ax(a≠0)的图象与反比例函致y=
如图,已知正比例函数y=ax(a≠0)的图象与反比例函致y=| k | x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 已知正比例函数y1=x,反比例函数y2=
已知正比例函数y1=x,反比例函数y2=| 1 |
| x |
| 1 |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 为M,又正比例函数y=kx的图象与二次函数相交于两点D、E,且P是线段DE的中点.
为M,又正比例函数y=kx的图象与二次函数相交于两点D、E,且P是线段DE的中点.| 93 |
| 16 |
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com