
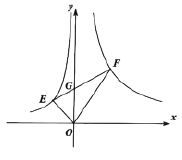
【题目】如图,在反比例函数![]() 与
与![]() 的图象上分别有一点
的图象上分别有一点![]() ,
,![]() ,连接
,连接![]() 交
交![]() 轴于点
轴于点![]() ,若
,若![]() 且
且![]() ,则
,则![]() __________.
__________.
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:
【题目】把二次涵数![]() 的图象先向左平移2个单位长度,再向上平移4个单位长度,得到二次函数
的图象先向左平移2个单位长度,再向上平移4个单位长度,得到二次函数![]() 的图象.
的图象.
(1)试确定![]() ,
,![]() ,
,![]() 的值;
的值;
(2)指出二次函数![]() 图象的开口方向、对称轴和顶点坐标.
图象的开口方向、对称轴和顶点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
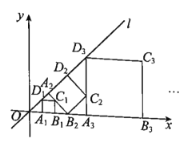
【题目】如图,在平面直角坐标系中,直线l为正比例函数![]() 的图象,点
的图象,点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作x轴的垂线交直线l于点
作x轴的垂线交直线l于点![]() ,以
,以![]() 为边作正方形
为边作正方形![]() ;过点
;过点![]() 作直线l的垂线,垂足为
作直线l的垂线,垂足为![]() ,交x轴于点
,交x轴于点![]() ,以
,以![]() 为边作正方形
为边作正方形![]() ;过点
;过点![]() 作x轴的垂线,垂足为
作x轴的垂线,垂足为![]() ,交直线l于点
,交直线l于点![]() ,以
,以![]() 为边作正方形
为边作正方形![]() ;……按此规律操作下去,得到的正方形
;……按此规律操作下去,得到的正方形![]() 的面积是______________.
的面积是______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD的边长为4,E为BC边上一点,BE=3,M为线段AE上一点,射线BM交正方形的一边于点F,且BF=AE,则BM的长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】梧桐山是深圳最高的山峰,某校综合实践活动小组要测量“主山峰”的高度,先在梧桐山对面广场的A处测得“峰顶”C的仰角为45°,此时,他们刚好与峰底D在同一水平线上.然后沿着坡度为30°的斜坡正对着“主山峰”前行700米,到达B处,再测得“峰顶”C的仰角为60°,如图,根据以上条件求出“主山峰”的高度?(测角仪的高度忽略不计,结果精确到1米).参考数据:(![]() 1.4,
1.4,![]() 1.7)
1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年6月12日,重庆直达香港高铁的车票正式开售据悉,重庆直达香港的这趟G319/320次高铁预计在7月份开行,全程1342公里只需7个半小时该车次沿途停靠站点包括遵义、贵阳东、桂林西、肇庆东、广州南和深圳北重庆直达香港高铁开通将为重庆旅游业发展增添生机与活力,预计重庆旅游经济将创新高在此之前技术部门做了大量测试,在一次测试中一高铁列车从![]() 地出发匀速驶向
地出发匀速驶向![]() 地,到达
地,到达![]() 地停止;同时一普快列车从
地停止;同时一普快列车从![]() 地出发,匀速驶向
地出发,匀速驶向![]() 地,到达
地,到达![]() 地停止且
地停止且![]() ,
,![]() 两地之间有一
两地之间有一![]() 地,其中
地,其中![]() ,如图①两列车与
,如图①两列车与![]() 地的距离之和
地的距离之和![]() (千米)与普快列车行驶时间
(千米)与普快列车行驶时间![]() (小时)之间的关系如图②所示则高铁列车到达
(小时)之间的关系如图②所示则高铁列车到达![]() 地时,普快列车离
地时,普快列车离![]() 地的距离为__________千米.
地的距离为__________千米.

查看答案和解析>>
科目:初中数学 来源: 题型:
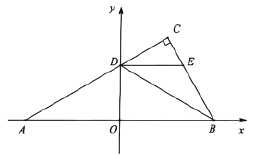
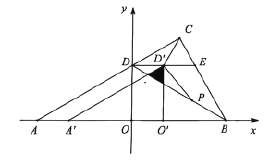
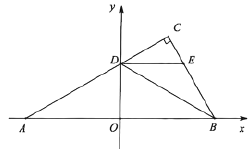
【题目】如图平面直角坐标系中,点![]() ,
,![]() 在
在![]() 轴上,
轴上,![]() ,点
,点![]() 在
在![]() 轴上方,
轴上方,![]() ,
,![]() ,线段
,线段![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() ,连接
,连接![]() ,
,![]() 平分
平分![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于
于![]() .
.
(1)点![]() 的坐标为 .
的坐标为 .
(2)将![]() 沿线段
沿线段![]() 向右平移得
向右平移得![]() ,当点
,当点![]() 与
与![]() 重合时停止运动,记
重合时停止运动,记![]() 与
与![]() 的重叠部分面积为
的重叠部分面积为![]() ,点
,点![]() 为线段
为线段![]() 上一动点,当
上一动点,当![]() 时,求
时,求![]() 的最小值;
的最小值;
(3)当![]() 移动到点
移动到点![]() 与
与![]() 重合时,将
重合时,将![]() 绕点
绕点![]() 旋转一周,旋转过程中,直线
旋转一周,旋转过程中,直线![]() 分别与直线
分别与直线![]() 、直线
、直线![]() 交于点
交于点![]() 、点
、点![]() ,作点
,作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,连接
,连接![]() 、
、![]() 、
、![]() .当
.当![]() 为直角三角形时,直接写出线段
为直角三角形时,直接写出线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.
(1)证明与推断:
①求证:四边形CEGF是正方形;
②推断:![]() 的值为 :
的值为 :
(2)探究与证明:
将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图(2)所示,试探究线段AG与BE之间的数量关系,并说明理由:
(3)拓展与运用:
正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图(3)所示,延长CG交AD于点H.若AG=6,GH=2![]() ,则BC= .
,则BC= .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com