
【题目】当﹣2≤x≤1时,二次函数y=﹣(x﹣m)2+m2+1有最大值4,则实数m的值为( )
A.﹣ ![]()
B.![]() 或﹣
或﹣ ![]()
C.2或﹣ ![]()
D.2或﹣ ![]() 或﹣
或﹣ ![]()
【答案】C
【解析】解:二次函数对称轴为直线x=m, ①m<﹣2时,x=﹣1取得最大值,﹣(﹣1﹣m)2+m2+1=4,
解得m=﹣2,不合题意,舍去;
②﹣2≤m≤1时,x=m取得最大值,m2+1=4,
解得m=± ![]() ,
,
∵m= ![]() 不满足﹣2≤m≤1的范围,
不满足﹣2≤m≤1的范围,
∴m=﹣ ![]() ;
;
③m>1时,x=1取得最大值,﹣(1﹣m)2+m2+1=4,
解得m=2.
综上所述,m=2或﹣ ![]() 时,二次函数有最大值4.
时,二次函数有最大值4.
故选:C.
【考点精析】本题主要考查了二次函数的最值的相关知识点,需要掌握如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a才能正确解答此题.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】某中学在“助残日”举行了一次“手拉手、献爱心”的捐款活动,学校对已捐款学生人数及捐款金额情况进行了调查.图①表示的是各年级捐款人数占总捐款人数的百分比;图②是学校对学生的捐款金额情况进行抽样调查并根据所得数据绘制的统计图

(1)学校对多少名学生的捐款金额情况进行了抽样调查?
(2)这组捐款金额数据的平均数、中位数各是多少?
(3)若该校九年级共有400名学生捐款,估计全校学生捐款总金额大约多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】推理填空:
如图所示,已知∠1 = ∠2,∠B = ∠C,可推得AB∥CD,

理由如下:
∵∠1 = ∠2(已知),且∠1 = ∠4(_____________________),
∴∠2 = ∠4(等量代换).
∴CE∥BF(__________________________).
∴∠_____= ∠3(________________________)
又∵∠B = ∠C(已知),
∴∠3= ∠B(等量代换),
∴AB∥CD(_____________________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E、F分别为边AB、CD的中点,AC是对角线,过点B作BG∥AC交DA的延长线于点G.
(1)求证:CE∥AF;
(2)若∠G=90°,求证:四边形CEAF是菱形.
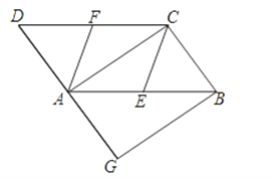
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按HUI图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)…根据这个规律,第2018个点的坐标为___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在直角坐标系中,
(1)请写出△ABC各点的坐标.
(2)若把△ABC向上平移2个单位,再向左平移1个单位得到△A′B′C′,写出 A′、B′、C′的坐标,并在图中画出平移后图形.
(3)求出三角形ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形MNPQ中,动点R从点N出发,沿着N→P→Q→M方向运动至点M处停止,设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则下列说法不正确的是( )

A.当x=2时,y=5
B.矩形MNPQ的面积是20
C.当x=6时,y=10
D.当y=![]() 时,x=10
时,x=10
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com