练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
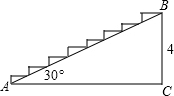
    4．现要把如图所示的楼梯铺上地毯，则所需地毯的长度约为（　　）（结果精确到0.1m）
    A．6.9mB．4mC．8mD．10.9m

    分析 要求地毯的长度其实就是求AC与BC的长度和．利用30°的正切函数求解．

    解答 解：∵坡角为30°，
    ∴AC=BC÷tan30°=$\sqrt{3}$×4=4$\sqrt{3}$．
    ∴AC+BC=（4+4$\sqrt{3}$）米≈4+4×1.73=4+6.92≈10.9（m）．
    故选D．

    点评 本题考查的是勾股定理的应用，将实际问题转化为直角三角形中的数学问题，可把条件和问题放到直角三角形中进行解决．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    14．如图，△ABC中，BE为AC边的中线，BF平分∠EBC，AQ⊥BF交BE于P，交BC于Q，求$\frac{EP}{CQ}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．计算：
    （1）3$\sqrt{3}$×$\sqrt{3}$；（2）$\sqrt{0.5}$×$\sqrt{24}$；（3）$\sqrt{45}$×$\frac{3}{2}$$\sqrt{\frac{2}{3}}$；
    （4）-$\frac{1}{2}$$\sqrt{xy}$×（-4$\sqrt{y}$）；（5）-$\frac{4}{3}$$\sqrt{18}$÷2$\sqrt{8}$×$\frac{1}{3}$$\sqrt{54}$；（6）-2$\sqrt{xy}$÷（-$\frac{3}{2x}\sqrt{{x}^{2}y}$×3$\sqrt{x}$）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

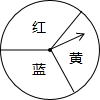    12．如果身边没有质地均匀的硬币，下列方法可以模拟掷硬币实验的是（　　）
    A．掷一个瓶盖，盖面朝上代表正面，盖面朝下代表反面
    B．掷一枚图钉，钉尖着地代表正面，钉帽着地代表反面
    C．掷一枚质地均匀的骰子，奇数点朝上代表正面，偶数点朝上代表反面
    D．转动如图所示的转盘，指针指向“红”代表正面，指针指向“蓝”代表反面

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．若4xmy3+（-2x2yn）=2xmyn，则nm=9．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．如图①是一个直角三角形纸片，∠C=Rt∠，AB=13cm，BC=5cm，将其折叠，使点C落在斜边上的点C′处，折痕为BD（如图②），则DC的长为（　　）
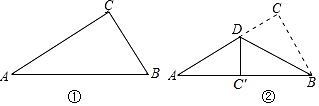
    A．$\frac{10}{3}$cmB．$\frac{8}{3}$cmC．$\frac{5}{2}$cmD．$\sqrt{5}$cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．如图，等边△ABC中，点D，E，F分别同时从点A，B，C出发，以相同的速度在AB，BC，CA上运动，连结DE，EF，DF．
    （1）证明：△DEF是等边三角形；
    （2）在运动过程中
    ①若△CEF是等边三角形，试求$\frac{{S}_{△DEF}}{{S}_{△ABC}}$的值；
    ②试问△CEF有可能是直角三角形吗？若有，请求出$\frac{{S}_{△DEF}}{{S}_{△ABC}}$的值；若没有，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

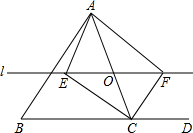    13．如图，在△ABC中，O是AC上的任意一点（不与点A、C重合），过点O平行于BC的直线l分别与∠BCA、∠DCA的平分线交于点E、F．
    （1）OE与OF相等吗？证明你的结论．
    （2）试确定点O的位置，使四边形AECF是矩形，并加以证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．已知抛物线y=x2+bx+c与x轴只有一个公共点为A（2，0），求抛物线与y轴的交点B的坐标．

    查看答案和解析>>

    同步练习册答案