
分析 题中没有指明该等腰三角形是锐角三角形还是钝角三角形,故应该分情况进行分析.
解答 解:显然三角形不可能为直角三角形,故分两种情况考虑:
(i)当三角形是锐角三角形时,高与另一腰的夹角为30°,则其顶角是60°,
所以该等腰三角形是等边三角形,腰是a,则底边上的高是$\frac{\sqrt{3}}{2}$a;
(ii)当三角形是钝角时,一腰上的高与另一腰的夹角为30°,
则等腰三角形的顶角的外角是60°,因而底角是30°,过顶角顶点作底边的垂线,则底边上的高是$\frac{1}{2}$a;
所以底边上的高是$\frac{\sqrt{3}}{2}$a或$\frac{1}{2}$a.
故答案为$\frac{\sqrt{3}}{2}$a或$\frac{1}{2}$a.
点评 此题考查了含30度角的直角三角形的性质以及等腰三角形的性质的综合运用.进行分类讨论是解题的关键.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
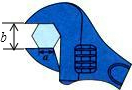 如图,要拧开一个边长为a(a=6mm)的正六边形,扳手张开的开口b至少为( )
如图,要拧开一个边长为a(a=6mm)的正六边形,扳手张开的开口b至少为( )| A. | 4$\sqrt{3}$mm | B. | 6$\sqrt{3}$mm | C. | 4$\sqrt{2}$mm | D. | 12mm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com