
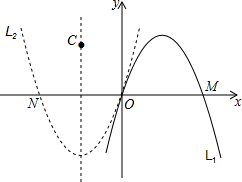
 ÔÚÖ±œÇŚű±êÏ”xOyÖĐŁŹ¶šÒć”ăCŁšaŁŹbŁ©ÎȘĆŚÎïÏßLŁșy=ax2+bxŁšaĄÙ0Ł©”ÄÌŰŐś”ăŚű±êŁź
ÔÚÖ±œÇŚű±êÏ”xOyÖĐŁŹ¶šÒć”ăCŁšaŁŹbŁ©ÎȘĆŚÎïÏßLŁșy=ax2+bxŁšaĄÙ0Ł©”ÄÌŰŐś”ăŚű±êŁź·ÖÎö Łš1Ł©œáșÏ”ăAĄąB”ă”ÄŚű±êŁŹÀûÓĂŽę¶šÏ”Êę·šŒŽżÉÇółöĆŚÎïÏßL”ÄșŻÊęœâÎöÊœŁŹÔÙœáșÏÌŰŐś”ă”ĶšÒ棏ŒŽżÉ”ĂłöœáÂÛŁ»
Łš2Ł©ąÙÓÉĆŚÎïÏßL1Łșy=ax2+bxÓëĆŚÎïÏßL2čŰÓÚÔ”ăO¶ÔłÆŁŹżÉœ«y»»łÉ-yŁŹœ«x»»łÉ-xŁŹŐûÀíșóŒŽżÉ”ĂłöœáÂÛŁ»
ąÚžùŸĘĆŚÎïÏßL2”ÄœâÎöÊœżÉŐÒłöËü”ĶԳÆÖáÎȘŁșx=$\frac{b}{2a}$ŁŹÓÉĆŚÎïÏßL1”ÄÌŰŐś”ăCÔÚĆŚÎïÏßL2”ĶԳÆÖáÉÏżÉ”Ăłöa=$\frac{b}{2a}$ŁŹ±äĐÎșóŒŽżÉ”ĂłöœáÂÛŁ»
ąÛœáșÏąÚ”ÄœáÂÛŁŹ±íÊŸłö”ăCĄąMĄąNÈę”ă”ÄŚű±êŁŹÓÉÁœ”ăŒä”ÄŸàÀëč«ÊœżÉ”ĂłöMNĄąMCĄąNC”Äł€¶ÈŁŹœáșÏ”ÈŃüÈęœÇĐΔÄĐÔÖÊ·ÖÈęÖÖÇéżöżŒÂÇŁŹ·Ö±đžùŸĘÏ߶ÎÏà”È”ĂłöčŰÓÚa”ÄÒ»ÔȘËĎηœłÌŁŹœâ·œłÌÔÙœáșÏa”Ä·¶Î§ŒŽżÉ”Ăłöa”ÄÖ”Łź
œâŽđ œâŁșŁš1Ł©œ«”ăAŁš-2ŁŹ-2Ł©ĄąBŁš-4ŁŹ0Ł©ŽúÈë”œĆŚÎïÏßœâÎöÊœÖĐŁŹ
”Ă$\left\{\begin{array}{l}{-2=4a-2b}\\{0=16a-4b}\end{array}\right.$ŁŹœâ”ĂŁș$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=2}\end{array}\right.$Łź
ĄàĆŚÎïÏßL”ÄœâÎöÊœÎȘy=$\frac{1}{2}{x}^{2}$+2xŁŹ
ĄàËü”ÄÌŰŐś”ăÎȘŁš$\frac{1}{2}$ŁŹ2Ł©Łź
Łš2Ł©ąÙĄßĆŚÎïÏßL1Łșy=ax2+bxÓëĆŚÎïÏßL2čŰÓÚÔ”ăO¶ÔłÆŁŹ
ĄàĆŚÎïÏßL2”ÄœâÎöÊœÎȘ-y=aŁš-xŁ©2+bŁš-xŁ©ŁŹŒŽy=-ax2+bxŁź
čÊŽđ°žÎȘŁșy=-ax2+bxŁź
ąÚĄßĆŚÎïÏßL2”ĶԳÆÖáÎȘÖ±Ïߣșx=-$\frac{b}{2ĄÁŁš-aŁ©}$=$\frac{b}{2a}$Łź
Ąà”±ĆŚÎïÏßL1”ÄÌŰŐś”ăCŁšaŁŹbŁ©ÔÚĆŚÎïÏßL2”ĶԳÆÖáÉÏʱŁŹÓĐa=$\frac{b}{2a}$ŁŹ
ĄàaÓëb”ÄčŰϔʜÎȘb=2a2Łź
ąÛĄßĆŚÎïÏßL1ĄąL2ÓëxÖáÓĐÁœžöȻ͏”Äœ»”ăMĄąNŁŹ
ĄàÔÚĆŚÎïÏßL1Łșy=ax2+bxÖĐŁŹÁîy=0ŁŹŒŽax2+bx=0ŁŹ
œâ”ĂŁșx1=-$\frac{b}{a}$ŁŹx2=0ŁšÉáÈ„Ł©ŁŹ
ŒŽ”ăMŁš-$\frac{b}{a}$ŁŹ0Ł©Ł»
ÔÚĆŚÎïÏßL2Łșy=-ax2+bxÖĐŁŹÁîy=0ŁŹŒŽ-ax2+bx=0ŁŹ
œâ”ĂŁșx1=$\frac{b}{a}$ŁŹx2=0ŁšÉáÈ„Ł©ŁŹ
ŒŽ”ăNŁš$\frac{b}{a}$ŁŹ0Ł©Łź
Ąßb=2a2ŁŹ
Ąà”ăMŁš-2aŁŹ0Ł©ŁŹ”ăNŁš2aŁŹ0Ł©ŁŹ”ăCŁšaŁŹ2a2Ł©Łź
ĄàMN=2a-Łš-2aŁ©=4aŁŹMC=$\sqrt{[a-Łš-2aŁ©]^{2}+4{a}^{4}}$ŁŹNC=$\sqrt{Łša-2aŁ©^{2}+4{a}^{4}}$Łź
ÒòŽËÒÔ”ăCĄąMĄąNÎȘ¶„”ă”ÄÈęœÇĐÎÊÇ”ÈŃüÈęœÇĐÎʱŁŹÓĐÒÔÏÂÈęÖÖżÉÄÜŁș
ŁšiŁ©MC=MNŁŹŽËʱÓĐŁș$\sqrt{[a-Łš-2aŁ©]^{2}+4{a}^{4}}$=4aŁŹŒŽ9a2+4a4=16a2ŁŹ
œâ”ĂŁșa=0ŁŹ»òa=ĄÀ$\frac{\sqrt{7}}{2}$ŁŹ
ĄßaŁŒ0ŁŹ
Ąàa=-$\frac{\sqrt{7}}{2}$Ł»
ŁšiiŁ©NC=MNŁŹŽËʱÓĐŁș$\sqrt{Łša-2aŁ©^{2}+4{a}^{4}}$=4aŁŹŒŽa2+4a4=16a2ŁŹ
œâ”ĂŁșa=0ŁŹ»òa=ĄÀ$\frac{\sqrt{15}}{2}$ŁŹ
ĄßaŁŒ0ŁŹ
Ąàa=-$\frac{\sqrt{15}}{2}$Ł»
ŁšiiiŁ©MC=NCŁŹŽËʱÓĐŁș$\sqrt{[a-Łš-2aŁ©]^{2}+4{a}^{4}}$=$\sqrt{Łša-2aŁ©^{2}+4{a}^{4}}$ŁŹŒŽ9a2=a2ŁŹ
œâ”ĂŁșa=0ŁŹ
ÓÖĄßaŁŒ0ŁŹ
ĄàŽËÇéżöČ»ŽæÔÚŁź
ŚÛÉÏËùÊöŁș”±ÒÔ”ăCĄąMĄąNÎȘ¶„”ă”ÄÈęœÇĐÎÊÇ”ÈŃüÈęœÇĐÎʱŁŹa”ÄÖ”ÎȘ-$\frac{\sqrt{7}}{2}$»ò-$\frac{\sqrt{15}}{2}$Łź
”ăÆÀ ±ŸÌâżŒČéÁËÀûÓĂŽę¶šÏ”Êę·šÇó¶țŽÎșŻÊęœâÎöÊœĄą¶țŽÎșŻÊę”ÄĐÔÖÊĄą”ÈŃüÈęœÇĐΔÄĐÔÖÊÒÔŒ°œâÒ»ÔȘžßŽÎ·œłÌŁŹœâÌâ”ÄčŰŒüÊÇŁșŁš1Ł©ÀûÓĂŽę¶šÏ”Êę·šÇó¶țŽÎșŻÊęœâÎöÊœŁ»Łš2Ł©ąÙĂś°ŚčŰÓÚÔ”ă¶ÔłÆ”ă”ÄÌŰŐśŁ»ąÚÀûÓöțŽÎșŻÊę”ÄĐÔÖÊŐÒłö¶ÔłÆÖáčŰϔʜŁ»ąÛ·ÖÇéżöÌÖÂÛÇóÖ”Łź±ŸÌâÊôÓÚÖĐ””Ì⣏ÄѶÈČ»ŽóŁŹœâŸöžĂÌâĐÍÌâÄżÊ±ŁŹÊŚÏÈžùŸĘÌŰŐś”ă”ĶšÒćŐÒłöaĄąbÖźŒä”ÄčŰÏ”ŁŹÔÙœáșÏÁœ”ăŒä”ÄŸàÀëč«ÊœÒÔŒ°”ÈŃüÈęœÇĐΔÄĐÔÖÊŐÒłöčŰÓÚa”ÄÒ»ÔȘžßŽÎ·œłÌŁŹœâ·œłÌŒŽżÉ”ĂłöœáÂÛŁź


 ÔĶÁżìł”Ï”ÁĐŽđ°ž
ÔĶÁżìł”Ï”ÁĐŽđ°ž
| Äꌶ | žßÖĐżÎłÌ | Äꌶ | łőÖĐżÎłÌ |
| žßÒ» | žßÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ | łőÒ» | łőÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ |
| žß¶ț | žß¶țĂâ·ŃżÎłÌÍÆŒöŁĄ | łő¶ț | łő¶țĂâ·ŃżÎłÌÍÆŒöŁĄ |
| žßÈę | žßÈęĂâ·ŃżÎłÌÍÆŒöŁĄ | łőÈę | łőÈęĂâ·ŃżÎłÌÍÆŒöŁĄ |
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșÌîżŐÌâ
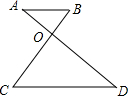 ÈçÍŒŁŹÏ߶ÎADÓëBCÏàœ»ÓÚ”ăOŁŹABĄÎCDŁŹÈôABŁșCD=2Łș3ŁŹĄśABO”ÄĂæ»ęÊÇ2ŁŹÔòĄśCDO”ÄĂæ»ę”ÈÓÚ4.5Łź
ÈçÍŒŁŹÏ߶ÎADÓëBCÏàœ»ÓÚ”ăOŁŹABĄÎCDŁŹÈôABŁșCD=2Łș3ŁŹĄśABO”ÄĂæ»ęÊÇ2ŁŹÔòĄśCDO”ÄĂæ»ę”ÈÓÚ4.5ŁźČ鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșÌîżŐÌâ
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșœâŽđÌâ
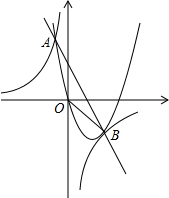 ÈçÍŒŁŹÖ±Ïßy=-2x+2ÓëĆŚÎïÏßy=ax2+bxŁšaŁŒ0Ł©Ïàœ»ÓÚ”ăAŁŹBŁźË«ÇúÏßy=$\frac{k}{x}$čęAĄąBÁœ”㣏ÒŃÖȘ”ăB”ÄŚű±êÎȘŁš2ŁŹ-2Ł©ŁŹ”ăAÔÚ”Ú¶țÏóÏȚÄÚŁŹÇÒtanĄÏAoy=$\frac{1}{4}$Łź
ÈçÍŒŁŹÖ±Ïßy=-2x+2ÓëĆŚÎïÏßy=ax2+bxŁšaŁŒ0Ł©Ïàœ»ÓÚ”ăAŁŹBŁźË«ÇúÏßy=$\frac{k}{x}$čęAĄąBÁœ”㣏ÒŃÖȘ”ăB”ÄŚű±êÎȘŁš2ŁŹ-2Ł©ŁŹ”ăAÔÚ”Ú¶țÏóÏȚÄÚŁŹÇÒtanĄÏAoy=$\frac{1}{4}$ŁźČ鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșœâŽđÌâ
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșœâŽđÌâ
 ÈçÍŒŁŹÔÚÆœĂæÖ±œÇŚű±êÏ”ÖĐŁŹĄÏOCA=90ĄăŁŹ”ăAÔÚxÖáÉÏŁŹOC=AC=4ŁŹDĄąE·Ö±đÊÇOCĄąAC”ÄÖД㣏œ«ËıßĐÎOAEDŃŰxÖáÏòÓÒÆœÒÆŁŹ”ĂËıßĐÎPQRSŁźÉèOP=mŁš0ŁŒmŁŒ4$\sqrt{2}$Ł©Łź
ÈçÍŒŁŹÔÚÆœĂæÖ±œÇŚű±êÏ”ÖĐŁŹĄÏOCA=90ĄăŁŹ”ăAÔÚxÖáÉÏŁŹOC=AC=4ŁŹDĄąE·Ö±đÊÇOCĄąAC”ÄÖД㣏œ«ËıßĐÎOAEDŃŰxÖáÏòÓÒÆœÒÆŁŹ”ĂËıßĐÎPQRSŁźÉèOP=mŁš0ŁŒmŁŒ4$\sqrt{2}$Ł©ŁźČ鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșœâŽđÌâ
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșŃĄÔńÌâ
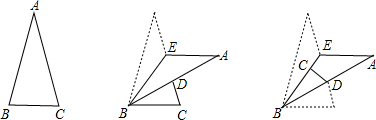
| AŁź | 75Ąă | BŁź | 76Ąă | CŁź | 77Ąă | DŁź | 78Ąă |
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșÌîżŐÌâ
 ÔÚÆœĐĐËıßĐÎABCDÖĐŁŹEÎȘAD”ÄÖД㣏ÈçčûAFŁșBF=2Łș5ŁŹÔò$\frac{AG}{GC}$=$\frac{2}{9}$Łź
ÔÚÆœĐĐËıßĐÎABCDÖĐŁŹEÎȘAD”ÄÖД㣏ÈçčûAFŁșBF=2Łș5ŁŹÔò$\frac{AG}{GC}$=$\frac{2}{9}$ŁźČ鿎Žđ°žșÍœâÎö>>
°Ù¶ÈÖÂĐĆ - Á·Ï°ČáÁбí - ÊÔÌâÁбí
șț±±ÊĄ»„ÁȘÍű΄·šșÍČ»ÁŒĐĆÏąŸÙ±šÆœÌš | ÍűÉÏÓĐșŠĐĆÏąŸÙ±šŚšÇű | ”çĐĆŐ©ÆŸÙ±šŚšÇű | ÉæÀúÊ·ĐéÎȚÖśÒćÓĐșŠĐĆÏąŸÙ±šŚšÇű | ÉæÆóÇÖÈšŸÙ±šŚšÇű
΄·šșÍČ»ÁŒĐĆÏąŸÙ±š”ç»°Łș027-86699610 ŸÙ±šÓÊÏäŁș58377363@163.com