
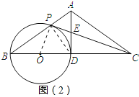
【题目】已知:如图![]() ,在
,在![]() 中,
中,![]() ,点
,点![]() 是边
是边![]() 的中点.以
的中点.以![]() 为直径作圆
为直径作圆![]() ,交边
,交边![]() 于点
于点![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() .
.
![]() 求证:
求证:![]() 是圆
是圆![]() 的切线;
的切线;
![]() 当
当![]() 时,求证:
时,求证:![]() ;
;
![]() 如图
如图![]() ,当
,当![]() 是圆
是圆![]() 的切线,
的切线,![]() 为
为![]() 中点,
中点,![]() ,求
,求![]() 的长.
的长.

【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据等腰三角形的三线合一的性质可得AD⊥BD,即可判定![]() 是圆
是圆![]() 的切线;(2)连接PD,根据直径所对的圆周角是直角可得∠BPD=90°,即可得PD∥AC;已知点D是边BC的中点,可得
的切线;(2)连接PD,根据直径所对的圆周角是直角可得∠BPD=90°,即可得PD∥AC;已知点D是边BC的中点,可得![]() =
=![]() BC;再由
BC;再由![]() ,可判定△BPD∽△BAC、△PED∽△CEA,根据相似三角形的性质可得
,可判定△BPD∽△BAC、△PED∽△CEA,根据相似三角形的性质可得![]() ,
,![]() ,即可证得
,即可证得![]() ;(3)(3)连接OP,可求得
;(3)(3)连接OP,可求得![]() ,
,![]() ,
,![]() ;根据切线的性质可得
;根据切线的性质可得![]() .根据由勾股定理求得
.根据由勾股定理求得![]() ;在
;在![]() 中可
中可![]() ,在Rt
,在Rt![]() 中,
中,![]() ,由此求得
,由此求得![]() .即可求得
.即可求得![]() .
.
根据三角函数可求得PC,CD的长,再在RT△ADE中利用三角函数求得DE的长,进而得出AD的长.
![]() 证明:∵
证明:∵![]() ,点
,点![]() 是边
是边![]() 的中点,
的中点,
∴![]() .
.
又∵![]() 是圆
是圆![]() 直径,
直径,
∴![]() 是圆
是圆![]() 的切线.
的切线.
![]() 证明:连接
证明:连接![]() ,则∠BPD=90°,
,则∠BPD=90°,
∵![]() ,
,
∴![]() ,
,
∵点D是边BC的中点,
∴![]() =
=![]() BC,
BC,
∵![]() ,
,
∴△BPD∽△BAC,△PED∽△CEA,
∴![]() ,
,![]()
∴![]() ;
;
![]() 连接
连接![]() ,
,
由![]() ,得
,得![]() ,
,![]() ,
,![]() ,
,
∵![]() 是圆
是圆![]() 的切线,
的切线,![]() 为圆心,
为圆心,
∴![]() .∴由勾股定理,得
.∴由勾股定理,得![]() ,
,
在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,
,![]() .
.
∵![]() 为
为![]() 中点,
中点,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】(1)已知y=(m2+m)![]() +(m﹣3)x+m2是x的二次函数,求出它的解析式.
+(m﹣3)x+m2是x的二次函数,求出它的解析式.
(2)用配方法求二次函数y=﹣x2+5x﹣7的顶点坐标并求出函数的最大值或最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度后,点B′恰好与点C重合,则平移的距离和旋转角的度数分别为( )

A.4,30° B.2,60° C.1,30° D.3,60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一元二次方程![]() ,下列说法:①若a+c=0,方程
,下列说法:①若a+c=0,方程![]() 有两个不等的实数根;②若方程
有两个不等的实数根;②若方程![]() 有两个不等的实数根,则方程
有两个不等的实数根,则方程![]() 也一定有两个不等的实数根;③若c是方程
也一定有两个不等的实数根;③若c是方程![]() 的一个根,则一定有
的一个根,则一定有![]() 成立;④若m是方程
成立;④若m是方程![]() 的一个根,则一定有
的一个根,则一定有![]() 成立.其中正确地只有 ( )
成立.其中正确地只有 ( )
A. ①② B. ②③ C. ③④ D. ①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形纸片ABCD中,已知AD=8,AB=6,E是边BC上的点,以AE为折痕折叠纸片,使点B落在点F处,连接FC,当△EFC为直角三角形时,BE的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个自然数的立方,可以分裂成若干个连续奇数的和。例如:![]() 和
和![]() 分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和,即
分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和,即![]() =3+5;
=3+5;![]() =7+9+11;
=7+9+11;![]() =13+15+17+19;…;若
=13+15+17+19;…;若![]() 也按照此规律来进行“分裂”,则
也按照此规律来进行“分裂”,则![]() “分裂”出的奇数中,最大的奇数是______.
“分裂”出的奇数中,最大的奇数是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线 y=2x2﹣4x+m 的图象的部分如图所示,则关于 x 的一元二次方程 2x2﹣4x+m=0 的解是 x1=______,x2=_________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com