
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别相交于点B、C,经过B、C两点的抛物线
轴分别相交于点B、C,经过B、C两点的抛物线![]() 与
与![]() 轴的另一个交点为A,顶点为P,且对称轴为直线
轴的另一个交点为A,顶点为P,且对称轴为直线![]() 。点G是抛物线
。点G是抛物线![]() 位于直线
位于直线![]() 下方的任意一点,连接PB、GB、GC、AC .
下方的任意一点,连接PB、GB、GC、AC .
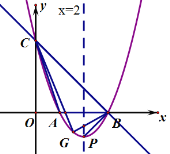
(1)求该抛物线的解析式;
(2)求△GBC面积的最大值;
(3)连接AC,在![]() 轴上是否存在一点Q,使得以点P,B,Q为顶点的三角形与△ABC相似?若存在,求出点Q的坐标;若不存在,请说明理由。
轴上是否存在一点Q,使得以点P,B,Q为顶点的三角形与△ABC相似?若存在,求出点Q的坐标;若不存在,请说明理由。
【答案】(1)![]() ; (2)当时
; (2)当时![]() ,
,![]() 面积的取最大值
面积的取最大值![]() ; (3)在x轴上存在两点Q1(0,0),Q2(
; (3)在x轴上存在两点Q1(0,0),Q2(![]() ,0),能使得以点P,B,Q为顶点的三角形与△ABC相似.
,0),能使得以点P,B,Q为顶点的三角形与△ABC相似.
【解析】
(1)根据二次函数的对称性,已知对称轴的解析式以及B点的坐标,即可求出A的坐标,利用抛物线过A、B、C三点,可用待定系数法来求函数的解析式;
(2)过![]() 作
作![]() ∥
∥![]() 轴交
轴交![]() 于点
于点![]() .设点
.设点![]()
![]() ,则点
,则点![]() ,列出关于△GBC面积的解析式,利用二次函数的性质求解即可;
,列出关于△GBC面积的解析式,利用二次函数的性质求解即可;
(3)本题要先根据抛物线的解析式求出顶点P的坐标,然后求出BP的长,进而分三情况进行讨论:①当![]() ,∠PBQ=∠ABC=45°时;②当
,∠PBQ=∠ABC=45°时;②当![]() ,∠QBP=∠ABC=45°时;③当Q在B点右侧,即可得出∠PBQ≠∠BAC,因此此种情况是不成立的,综上所述即可得出符合条件的Q的坐标.
,∠QBP=∠ABC=45°时;③当Q在B点右侧,即可得出∠PBQ≠∠BAC,因此此种情况是不成立的,综上所述即可得出符合条件的Q的坐标.
(1)∵直线y=﹣x+3与x轴相交于点B、点C,
∴当y=0时,x=3;当x=0时,y=3.
∴点B的坐标为(3,0),点C的坐标为(0,3),
又∵抛物线过x轴上的A,B两点,且对称轴为x=2,
∴点A的坐标为(1,0).
又∵抛物线y=ax2+bx+c过点A(1,0),B(3,0),C(0,3),
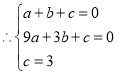 , 解得:
, 解得: ,
,
∴该抛物线的解析式为:![]() ;
;
(2)如图,过![]() 作
作![]() ∥
∥![]() 轴交
轴交![]() 于点
于点![]() .
.
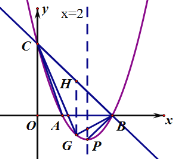
设点![]()
![]() ,则点
,则点![]() ,
,
∴![]() ,
,
∴![]()
![]() ,
,
∵![]() ,
,
∴ 当时![]() ,
,![]() 面积的取最大值
面积的取最大值![]() .
.
(3)如图,
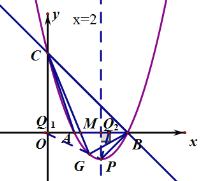
由y=x2﹣4x+3=(x﹣2)2﹣1,得顶点P(2,﹣1),
设抛物线的对称轴交x轴于点M,
∵在Rt△PBM中,PM=MB=1,
∴∠PBM=45°,PB=![]() .
.
由点B(3,0),C(0,3)易得OB=OC=3,在等腰直角三角形OBC中,∠ABC=45°,
由勾股定理,得BC=![]() .
.
假设在x轴上存在点Q,使得以点P,B,Q为顶点的三角形与△ABC相似.
①当![]() ,∠PBQ=∠ABC=45°时,△PBQ∽△ABC.
,∠PBQ=∠ABC=45°时,△PBQ∽△ABC.
即![]() ,
,
解得:BQ=3,
又∵BO=3,
∴点Q与点O重合,
∴Q1的坐标是(0,0).
②当![]() ,∠QBP=∠ABC=45°时,△QBP∽△ABC.
,∠QBP=∠ABC=45°时,△QBP∽△ABC.
即![]() ,
,
解得:QB=![]() .
.
∵OB=3,
∴OQ=OB﹣QB=3﹣![]() ,
,
∴Q2的坐标是(![]() ,0).
,0).
③当Q在B点右侧,
则∠PBQ=![]() =135°,∠BAC<135°,
=135°,∠BAC<135°,
故∠PBQ≠∠BAC.
则点Q不可能在B点右侧的x轴上,
综上所述,在x轴上存在两点Q1(0,0),Q2(![]() ,0),能使得以点P,B,Q为顶点的三角形与△ABC相似.
,0),能使得以点P,B,Q为顶点的三角形与△ABC相似.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系xOy中,点A(0,2),正方形OABC的顶点B在函数![]() (k ≠ 0,x<0) 的图象上,直线
(k ≠ 0,x<0) 的图象上,直线![]() :
:![]() 与函数
与函数![]() (k ≠ 0,x<0) 的图象交于点D,与x轴交于点E.
(k ≠ 0,x<0) 的图象交于点D,与x轴交于点E.
(1)求k的值;
(2)横、纵坐标都是整数的点叫做整点.
①当一次函数![]() 的图象经过点A时,直接写出△DCE内的整点的坐标;
的图象经过点A时,直接写出△DCE内的整点的坐标;
②若△DCE内的整点个数恰有6个,结合图象,求b的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
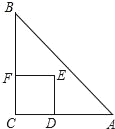
【题目】如图,Rt△ABC中,AC=BC=2,正方形CDEF的顶点D、F分别在AC、BC边上,设CD的长度为x,△ABC与正方形CDEF重叠部分的面积为y,则下列图象中能表示y与x之间的函数关系的是( )
A. 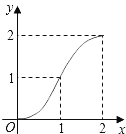 B.
B. 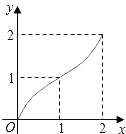
C. 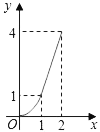 D.
D. 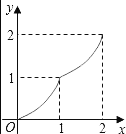
查看答案和解析>>
科目:初中数学 来源: 题型:
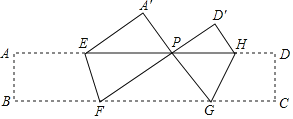
【题目】如图,把矩形ABCD沿EF,GH折叠,使点B,C落在AD上同一点P处,∠FPG=90°,△A′EP的面积是8![]() ,△D′PH的面积是4
,△D′PH的面积是4![]() ,则矩形ABCD的面积等于_____.
,则矩形ABCD的面积等于_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
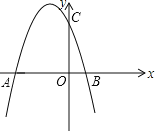
【题目】如图,抛物线y=ax2+bx+3与x轴交于A(﹣3,0),B(l,0)两点,与y轴交于点C.
(1)求抛物线的解析式;
(2)点P是抛物线上的动点,且满足S△PAO=2S△PCO,求出P点的坐标;
(3)连接BC,点E是x轴一动点,点F是抛物线上一动点,若以B、C、E、F为顶点的四边形是平行四边形时,请直接写出点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
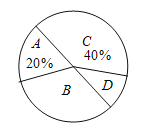
【题目】对某校学生寒假阅读时间情况调查,抽样统计绘制了两幅不完整的统计图,请结合信息解决下列问题:
阅读时间(小时) |
|
|
|
|
人数 | 60 | 80 |
(1)这次统计A类 人;D类 人;
(2)如果该校有1200学生,那么D类学生数量约为多少人?
(3)甲、乙、丙、丁4名学生是阅读属于D类学生,他们分别来自九年级1人,八年级1人,七年级2人,现抽取2人电话回访,则抽取到2人同为七年级学生的概率为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
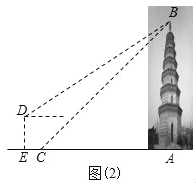
【题目】如图(1),在豫西南邓州市大十字街西南方,耸立着一座古老建筑-福胜寺梵塔,建于北宋天圣十年(公元1032年),学完了三角函数知识后,某校“数学社团”的刘明和王华决定用自己学到的知识测量“福胜寺梵塔”的高度.如图(2),刘明在点C处测得塔顶B的仰角为45°,王华在高台上的点D处测得塔顶B的仰角为40°,若高台DE高为5米,点D到点C的水平距离EC为1.3米,且A、C、E三点共线,求该塔AB的高度.(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,结果保留整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
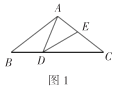
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上的一个动点(不与
边上的一个动点(不与![]() ,
,![]() 重合),以
重合),以![]() 为边作
为边作![]() ,交
,交![]() 边于点
边于点![]() .设
.设![]() ,
,![]() .今天我们将根据学习函数的经验,研究函数值
.今天我们将根据学习函数的经验,研究函数值![]() 随自变量
随自变量![]() 的变化而变化的规律.
的变化而变化的规律.
下面是某同学做的一部分研究结果,请你一起参与解答:
(1)自变量![]() 的取值范围是 ;
的取值范围是 ;
(2)通过计算,得到![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
| 0.5 | 1 | 1.5 | 2 | 3 | 4 | 4.5 | 5 | 5.5 |
| 3.3125 | 2.75 | 2.3125 | 2 | 2.3125 | 2.75 | 3.3125 |
请你补全表格;
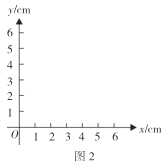
(3)在如图2所示的平面直角坐标系中,画出该函数的大致图象;
(4)根据图象,请写出该函数的一条性质.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(![]() ,0)和(m,y),对称轴为直线x=﹣1,下列5个结论:其中正确的结论为_____.(注:只填写正确结论的序号)①abc>0;②a+2b+4c=0;③2a﹣b>0;④3b+2c>0;⑤a﹣b≥m(am﹣b)
,0)和(m,y),对称轴为直线x=﹣1,下列5个结论:其中正确的结论为_____.(注:只填写正确结论的序号)①abc>0;②a+2b+4c=0;③2a﹣b>0;④3b+2c>0;⑤a﹣b≥m(am﹣b)
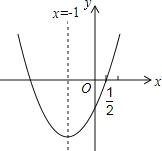
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com