练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，正方形的对角线交于点点，分别在，上（）且，，的延长线交于点，，的延长线交于点，连接.

    （1）求证：.

    （2）若正方形的边长为4，为的中点，求的长.

    【答案】（1）见解析（2）

    【解析】

    （1）证△OAM≌△OBN即可得；

    （2）作OH⊥AD，由正方形的边长为4且E为OM的中点知OH=HA=2、HM=4，再根据勾股定理得OM=2，由直角三角形性质知MN=OM．

    （1）∵四边形ABCD是正方形，

    ∴OA=OB，∠DAO=45°，∠OBA=45°，

    ∴∠OAM=∠OBN=135°，

    ∵∠EOF=90°，∠AOB=90°，

    ∴∠AOM=∠BON，

    ∴△OAM≌△OBN（ASA），

    ∴OM=ON；

    （2）如图，过点O作OH⊥AD于点H，

    ∵正方形的边长为4，

    ∴OH=HA=2，

    ∵E为OM的中点，

    ∴HM=4，

    则OM=，

    ∴MN=OM=2．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】密码锁有三个转轮，每个转轮上有十个数字：0，1，2，…9．小黄同学是9月份中旬出生，用生日“月份+日期”设置密码：9××

    小张同学要破解其密码：

    （1）第一个转轮设置的数字是9，第二个转轮设置的数字可能是　 　．

    （2）请你帮小张同学列举出所有可能的密码，并求密码数能被3整除的概率；

    （3）小张同学是6月份出生，根据（1）（2）的规律，请你推算用小张生日设置的密码的所有可能个数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，AC＝4cm，BC＝3cm，点P由B出发沿BA的方向向点A匀速运动，速度为1cm/s，同时点Q由A出发沿AC的方向向点C匀速运动，速度为2cm/s，连接PQ，设运动的时间为t（s），其中0＜t＜2，解答下列问题：

    （1）当t为何值时，以P、Q、A为顶点的三角形与△ABC相似？

    （2）是否存在某一时刻t，线段PQ将△ABC的面积分成1：2两部分？若存在，求出此时的t，若不存在，请说明理由；

    （3）点P、Q在运动的过程中，△CPQ能否成为等腰三角形？若能，请求出此时t的值，若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

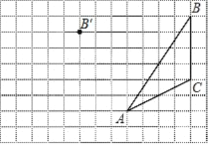
    【题目】画图并填空：如图，方格纸中每个小正方形的边长都为1．在方格纸内将△ABC经过一次平移后得到△A′B′C′，图中标出了点B的对应点B′．

    （1）在给定方格纸中画出平移后的△A′B′C′；

    （2）画出AB边上的中线CD

    （3）画出BC边上的高线AE

    （4）点为方格纸上的格点(异于点)，若，则图中的格点共有 个．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】完成下面推理过程：

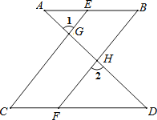
    如图，已知∠1=∠2，∠B=∠C，可推得AB∥CD．理由如下：

    ∵∠1=∠2（已知），

    且∠1=∠CGD（　 　），

    ∴∠2=∠CGD（ 　 　 ）．

    ∴CE∥BF（　 　）．

    ∴∠　 　=∠C（　 　）．

    又∵∠B=∠C（已知），

    ∴∠　 　=∠B（等量代换）．

    ∴AB∥CD（　 　）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在正方形ABCD的外侧，作等边三角形ADE，连接BE，CE．

    （1）求证：BE=CE．

    （2）求∠BEC的度数

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD是平行四边形，P是CD上一点，且AP和BP分别平分∠DAB和∠CBA.

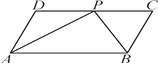
    (1)求∠APB的度数；

    (2)如果AD＝5 cm，AP＝8 cm，求△APB的周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠A=90°，AB=AC，BC=20，DE是△ABC的中位线，点M是边BC上一点，BM=3，点N是线段MC上的一个动点，连接DN，ME，DN与ME相交于点O．若△OMN是直角三角形，则DO的长是______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知∠1＋∠2＝180o, ∠3＝∠B，试说明∠DEC＋∠C＝180o.请完成下列填空：

    解：∵∠1＋∠2＝180o(已知)

    又∵∠1＋∠4＝180o(平角定义)

    ∴∠2＝∠4(________)

    ∴______∥______(_________)

    ∴∠3 ＝ ∠ADE(__________)

    又∵∠3＝∠B(已知)

    ∴∠ADE＝∠B(等量代换)

    ∴BC∥_____(_________)

    ∴∠DEC＋∠C＝180o(__________)

    查看答案和解析>>

    同步练习册答案