
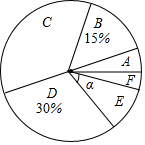
 今年四月份,某校在孝感市争创“全国文明城市”活动中,组织全体学生参加了“弘扬孝德文化,争做文明学生”的知识竞赛,赛后随机抽取了部分参赛学生的成绩,按得分划分成A,B,C,D,E,F六个等级,并绘制成如下两幅不完整的统计图表.
今年四月份,某校在孝感市争创“全国文明城市”活动中,组织全体学生参加了“弘扬孝德文化,争做文明学生”的知识竞赛,赛后随机抽取了部分参赛学生的成绩,按得分划分成A,B,C,D,E,F六个等级,并绘制成如下两幅不完整的统计图表.| 等级 | 得分x(分) | 频数(人) |
| A | 95≤x≤100 | 4 |
| B | 90≤x<95 | m |
| C | 85≤x<90 | n |
| D | 80≤x<85 | 24 |
| E | 75≤x<80 | 8 |
| F | 70≤x<75 | 4 |
分析 (1)由D等级人数及其百分比求得总人数,总人数乘以B等级百分比求得其人数,根据各等级人数之和等于总人数求得n的值,360度乘以E等级人数所占比例可得;
(2)画出树状图即可解决问题.
解答 解:(1)本次抽样调查样本容量为24÷30%=80,
则m=80×15%=12,n=80-(4+12+24+8+4)=28,
扇形统计图中,E等级对应扇形的圆心角α=360°×$\frac{8}{80}$=36°,
故答案为:80,12,8,36;
(2)树状图如图所示,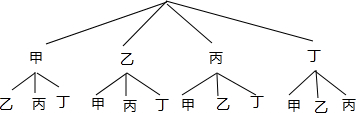
∵从四人中随机抽取两人有12种可能,恰好是甲和乙的有2种可能,
∴抽取两人恰好是甲和乙的概率是$\frac{1}{6}$.
点评 本题考查列表法、树状图法、扇形统计图、频数分布表等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 某商店经销一种品牌的洗衣机,其中某一型号的洗衣机每台进价为a元,商店将进价提高20%后作为零售价进行销售,一段时间后,商店又以9折优惠价促销,这时该型号洗衣机的零售价为1.08a元.
某商店经销一种品牌的洗衣机,其中某一型号的洗衣机每台进价为a元,商店将进价提高20%后作为零售价进行销售,一段时间后,商店又以9折优惠价促销,这时该型号洗衣机的零售价为1.08a元.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 “赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若(a+b)2=21,大正方形的面积为13,则小正方形的面积为( )
“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若(a+b)2=21,大正方形的面积为13,则小正方形的面积为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 调查孝感区居民对创建“全国卫生城市”的知晓度,宜采用抽样调查 | |
| B. | 一组数据85,95,90,95,95,90,90,80,95,90的众数为95 | |
| C. | “打开电视,正在播放乒乓球比赛”是必然事件 | |
| D. | 同时抛掷两枚质地均匀的硬币一次,出现两个正面朝上的概率为$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
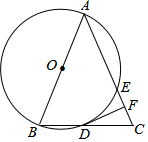 如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC、AC分别交于D、E两点,过点D作DF⊥AC,垂足为点F.
如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC、AC分别交于D、E两点,过点D作DF⊥AC,垂足为点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
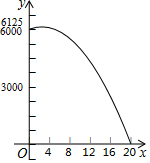 某商品的进价为每件40元,当售价为每件60元时,每星期可卖出300件,现需降价处理,且经市场调查,每降价1元,每星期可多卖出20件,在确保盈利的前提下,解答下列问题:
某商品的进价为每件40元,当售价为每件60元时,每星期可卖出300件,现需降价处理,且经市场调查,每降价1元,每星期可多卖出20件,在确保盈利的前提下,解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com