
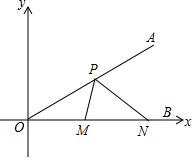
 如图,∠AOB的边OB与x轴正半轴重合,点P是OA上的一动点,点N(3,0)是OB上的一定点,点M是ON的中点,∠AOB=30°,要使PM+PN最小,则点P的坐标为($\frac{3}{2}$,$\frac{\sqrt{3}}{2}$).
如图,∠AOB的边OB与x轴正半轴重合,点P是OA上的一动点,点N(3,0)是OB上的一定点,点M是ON的中点,∠AOB=30°,要使PM+PN最小,则点P的坐标为($\frac{3}{2}$,$\frac{\sqrt{3}}{2}$). 分析 作N关于OA的对称点N′,连接N′M交OA于P,则此时,PM+PN最小,由作图得到ON=ON′,∠N′ON=2∠AON=60°,求得△NON′是等边三角形,根据等边三角形的性质得到N′M⊥ON,解直角三角形即可得到结论.
解答 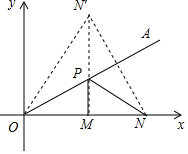 解:作N关于OA的对称点N′,连接N′M交OA于P,
解:作N关于OA的对称点N′,连接N′M交OA于P,
则此时,PM+PN最小,
∵OA垂直平分NN′,
∴ON=ON′,∠N′ON=2∠AON=60°,
∴△NON′是等边三角形,
∵点M是ON的中点,
∴N′M⊥ON,
∵点N(3,0),
∴ON=3,
∵点M是ON的中点,
∴OM=1.5,
∴PM=$\frac{\sqrt{3}}{2}$,
∴P($\frac{3}{2}$,$\frac{\sqrt{3}}{2}$).
故答案为:($\frac{3}{2}$,$\frac{\sqrt{3}}{2}$).
点评 本题考查了轴对称-最短路线问题,等边三角形的判定和性质,解直角三角形,关键是确定P的位置.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:解答题
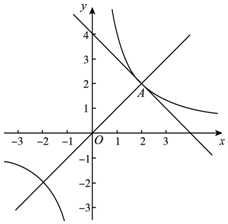 如图,在平面直角坐标系xOy中,反比例函数y=$\frac{k}{x}$(k≠0)与一次函数y=ax+4(a≠0)的图象只有一个公共点A(2,2),直线y=mx(m≠0)也过点A.
如图,在平面直角坐标系xOy中,反比例函数y=$\frac{k}{x}$(k≠0)与一次函数y=ax+4(a≠0)的图象只有一个公共点A(2,2),直线y=mx(m≠0)也过点A.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
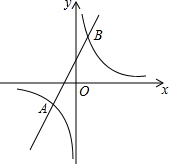 如图,直线y=2x+4与反比例函数y=$\frac{k}{x}$的图象相交于A(-3,a)和B两点
如图,直线y=2x+4与反比例函数y=$\frac{k}{x}$的图象相交于A(-3,a)和B两点查看答案和解析>>
科目:初中数学 来源: 题型:解答题
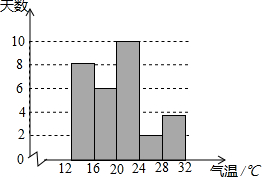 为了解某地某个季度的气温情况,用适当的抽样方法从该地这个季度中抽取30天,对每天的最高气温x(单位:℃)进行调查,并将所得的数据按照12≤x<16,16≤x<20,20≤x<24,24≤x<28,28≤x<32分成五组,得到如图频数分布直方图.
为了解某地某个季度的气温情况,用适当的抽样方法从该地这个季度中抽取30天,对每天的最高气温x(单位:℃)进行调查,并将所得的数据按照12≤x<16,16≤x<20,20≤x<24,24≤x<28,28≤x<32分成五组,得到如图频数分布直方图.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
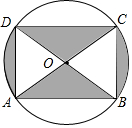 如图是某商品的标志图案,AC与BD是⊙O的两条直径,首尾顺次连接点A,B,C,D,得到四边形ABCD.若AC=10cm,∠BAC=36°,则图中阴影部分的面积为( )
如图是某商品的标志图案,AC与BD是⊙O的两条直径,首尾顺次连接点A,B,C,D,得到四边形ABCD.若AC=10cm,∠BAC=36°,则图中阴影部分的面积为( )| A. | 5πcm2 | B. | 10πcm2 | C. | 15πcm2 | D. | 20πcm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com