
 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:解答题
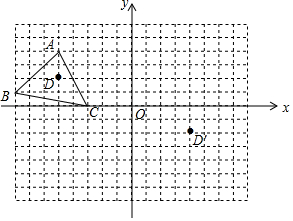 如图,把方格纸中的△ABC平移,使点D平移到点D′的位置,
如图,把方格纸中的△ABC平移,使点D平移到点D′的位置,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 数据3、5、4、1、-2的中位数是3 | |
| B. | 数据1、1、0、2、4的平均数是2 | |
| C. | 在选举中,人们通常最关心是数据的众数 | |
| D. | 甲乙两人近5次数学考试平均分都是95分,方差分别是2.5和8.5,要选一人参加数学竞赛,选甲比较合适 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | A+B是关于x的5次多项式 | B. | A-B是关于x的4次多项式 | ||
| C. | AB是关于x的10次多项式 | D. | $\frac{A}{B}$是与x无关的常数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
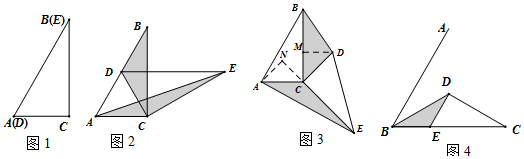
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
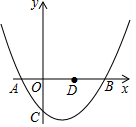 如图,已知抛物线y=$\frac{1}{2}$x2+bx+c(b、c是常数,且c<0)与x轴交于A、B两点(点A在点B的左侧),与y轴的负半轴交于点C,且OB=2OC.
如图,已知抛物线y=$\frac{1}{2}$x2+bx+c(b、c是常数,且c<0)与x轴交于A、B两点(点A在点B的左侧),与y轴的负半轴交于点C,且OB=2OC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com