
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 首先根据线段的中垂线上的点到线段两端点的距离相等,求出AB的中垂线与x轴的交点,即可求出点C1的坐标;然后再求出AB的长,以点A为圆心,以AB的长为半径画弧,与x轴的交点为点C2、C3;最后判断出以点B为圆心,以AB的长为半径画弧,与x轴没有交点,据此判断出点C的个数为多少即可.
解答 解:如图,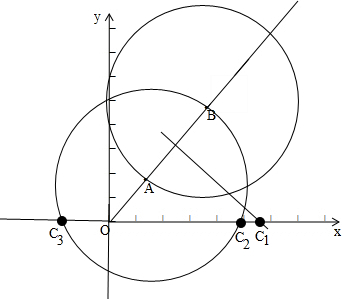 ,
,
∵AB所在的直线是y=x,
∴设AB的中垂线所在的直线是y=-x+b,
∵点A($\sqrt{2}$,$\sqrt{2}$),B(3$\sqrt{2}$,3$\sqrt{2}$),
∴AB的中点坐标是(2$\sqrt{2}$,2$\sqrt{2}$),
把x=2$\sqrt{2}$,y=2$\sqrt{2}$代入y=-x+b,
解得b=4$\sqrt{2}$,
∴AB的中垂线所在的直线是y=-x+4$\sqrt{2}$,
∴C1(4$\sqrt{2}$,0)
以点A为圆心,以AB的长为半径画弧,与x轴的交点为点C2、C3;
AB=$\sqrt{{(3\sqrt{2}-\sqrt{2})}^{2}{+(3\sqrt{2}-\sqrt{2})}^{2}}$=4,
∵3$\sqrt{2}$>4,
∴以点B为圆心,以AB的长为半径画弧,与x轴没有交点.
综上,可得
若以A、B、C三点为顶点的三角形是等腰三角形,则点C的个数为3.
故选:B.
点评 (1)此题主要考查了等腰三角形的性质和应用,考查了分类讨论思想的应用,要熟练掌握,解答此题的关键是要明确:①等腰三角形的两腰相等.②等腰三角形的两个底角相等.③等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.
(2)此题还考查了坐标与图形性质,要熟练掌握,解答此题的关键是要明确:到x轴的距离与纵坐标有关,到y轴的距离与横坐标有关;②距离都是非负数,而坐标可以是负数,在由距离求坐标时,需要加上恰当的符号.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:选择题
| A. | 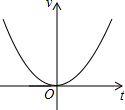 | B. |  | C. | 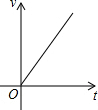 | D. | 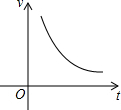 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
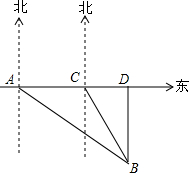 如图,新城区新建了三个商业城A,B,C,其中C在A的正东方向,在A处测得B在A的南偏东52°的方向,在C处测得B在C的南偏东26°的方向,已知A和B的距离是1000m.现有甲、乙两个工程对修建道路,甲修建一条从A到C的笔直道路AC,乙修建一条从B到直线AC最近的道路BD.求甲、乙修建的道路各是多长.(结果精确到1m)(参考数据:sin38°≈0.62,cos38°≈0.79,tan38°≈0.78,sin64°≈0.90,cos64°≈0.44,tan64°≈2.05)
如图,新城区新建了三个商业城A,B,C,其中C在A的正东方向,在A处测得B在A的南偏东52°的方向,在C处测得B在C的南偏东26°的方向,已知A和B的距离是1000m.现有甲、乙两个工程对修建道路,甲修建一条从A到C的笔直道路AC,乙修建一条从B到直线AC最近的道路BD.求甲、乙修建的道路各是多长.(结果精确到1m)(参考数据:sin38°≈0.62,cos38°≈0.79,tan38°≈0.78,sin64°≈0.90,cos64°≈0.44,tan64°≈2.05)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
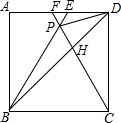 如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H.给出下列结论:
如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H.给出下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,海中一小岛上有一个观测点A,某天上午9:00观测到某渔船在观测点A的西南方向上的B处跟踪鱼群由南向北匀速航行.当天上午9:30观测到该渔船在观测点A的北偏西60°方向上的C处.若该渔船的速度为每小时30海里,在此航行过程中,问该渔船从B处开始航行多少小时,离观测点A的距离最近?(计算结果用根号表示,不取近似值).
如图,海中一小岛上有一个观测点A,某天上午9:00观测到某渔船在观测点A的西南方向上的B处跟踪鱼群由南向北匀速航行.当天上午9:30观测到该渔船在观测点A的北偏西60°方向上的C处.若该渔船的速度为每小时30海里,在此航行过程中,问该渔船从B处开始航行多少小时,离观测点A的距离最近?(计算结果用根号表示,不取近似值).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 30,27 | B. | 30,29 | C. | 29,30 | D. | 30,28 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com