
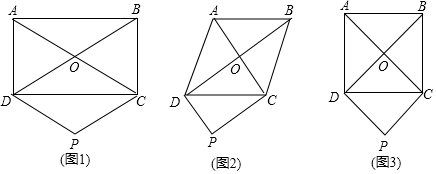
分析 (1)根据矩形的性质得出OD=OC,根据有一组对边平行且相等的四边形是平行四边形得出四边形CODP是平行四边形,根据菱形的判定推出即可;
(2)根据菱形的性质得出∠DOC=90°,根据有一组对边平行且相等的四边形是平行四边形得出四边形CODP是平行四边形,根据矩形的判定推出即可;
(3)根据正方形的性质得出OD=OC,∠DOC=90°,根据有一组对边平行且相等的四边形是平行四边形得出四边形CODP是平行四边形,根据正方形的判定推出即可;
解答 解:(1)四边形CODP的形状是菱形,理由如下:
∵四边形ABCD是矩形,
∴AC=BD,OA=OC=$\frac{1}{2}$AC,OB=OD=$\frac{1}{2}$BD,
∴OC=OD,
∵DP∥OC,DP=OC,
∴四边形CODP是平行四边形,
∵OC=OD,
∴平行四边形CODP是菱形;
(2)四边形CODP的形状是矩形,理由如下:
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠DOC=90°,
∵DP∥OC,DP=OC,
∴四边形CODP是平行四边形,
∵∠DOC=90°,
∴平行四边形CODP是矩形;
(3)四边形CODP的形状是正方形,理由如下:
∵四边形ABCD是正方形,
∴AC⊥BD,AC=BD,OA=OC=$\frac{1}{2}$AC,OB=OD=$\frac{1}{2}$BD,
∴∠DOC=90°,OD=OC,
∵DP∥OC,DP=OC,
∴四边形CODP是平行四边形,
∵∠DOC=90°,OD=OC
∴平行四边形CODP是正方形.
点评 本题是四边形综合题目,考查了平行四边形的判定,矩形、菱形、正方形的性质和判定,主要考查学生的猜想能力和推理能力,题目具有一定的代表性,是一道比较好的题目.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:选择题
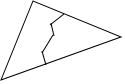 小丽不小心打碎了一块玻璃(如图),玻璃店老板根据涂总阴影部分重新划出一块与原来的玻璃完全相同的玻璃,其根据是( )
小丽不小心打碎了一块玻璃(如图),玻璃店老板根据涂总阴影部分重新划出一块与原来的玻璃完全相同的玻璃,其根据是( )| A. | SAS | B. | SSS | C. | ASA | D. | AAS |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (1,3) | B. | (3,1) | C. | (2,1) | D. | (3,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
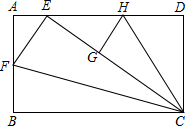 如图矩形ABCD是一张标准纸,长BC=AD=$\sqrt{2}$,AB=CD=1,把△BCF沿CF对折使点B恰好落在边AD上的点E处,再把△DCH沿CH对折使点D落在线段CE上的点G处.
如图矩形ABCD是一张标准纸,长BC=AD=$\sqrt{2}$,AB=CD=1,把△BCF沿CF对折使点B恰好落在边AD上的点E处,再把△DCH沿CH对折使点D落在线段CE上的点G处.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com