
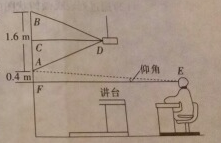
 教室的屏幕AB、投影仪D及教室中间前排学生位置左视图如图所示,为了确保眼睛不易疲劳,安装时要求教室中间前排学生与屏幕的距离≥屏幕高度的2倍.现测得屏幕的高度AB=1.6m,在屏幕的正中央C的前方放的投影仪离屏幕的距离CD=2m,前排学生的眼睛E看屏幕底端A的仰角∠AEF=6°,屏幕底端A到水平线EF的距离AF=0.4m.
教室的屏幕AB、投影仪D及教室中间前排学生位置左视图如图所示,为了确保眼睛不易疲劳,安装时要求教室中间前排学生与屏幕的距离≥屏幕高度的2倍.现测得屏幕的高度AB=1.6m,在屏幕的正中央C的前方放的投影仪离屏幕的距离CD=2m,前排学生的眼睛E看屏幕底端A的仰角∠AEF=6°,屏幕底端A到水平线EF的距离AF=0.4m.分析 (1)首先证明DB=DA,推出∠CDB=∠CDA,在Rt△ACD中,由tan∠ADC=$\frac{AC}{CD}$=$\frac{0.8}{2}$=0.4,推出∠ADC=22°,可得∠BDA=2∠ADC=44°;
(2)在Rt△AEF中,求出EF即可判断;
解答 解:(1) ∵AC=BC=0,8,DC⊥AB,
∵AC=BC=0,8,DC⊥AB,
∴DB=DA,
∴∠CDB=∠CDA,
在Rt△ACD中,tan∠ADC=$\frac{AC}{CD}$=$\frac{0.8}{2}$=0.4,
∴∠ADC=22°,
∴∠BDA=2∠ADC=44°,
(2)在Rt△AEF中,tan6°=$\frac{AF}{EF}$,
∴EF=$\frac{0.4}{0.11}$≈3.6,
∵3.6>2×1.6,
∴教室中间前排学生与屏幕的距离EF是合理的.
点评 本题考查解直角三角形的应用-仰角俯角问题、等腰三角形的有的和性质,锐角三角函数等知识,解题的关键是正确寻找直角三角形解决问题,属于中考常考题型.


 全能练考卷系列答案
全能练考卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 18×104 | B. | 1.8×105 | C. | 1.8×106 | D. | 18×105 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
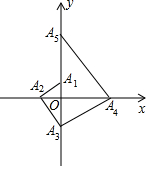 如图,点A1的坐标为(0,1),A2在x轴的负半轴上,且∠A1A2O=30°,过点A2作A2A3⊥A1A2,垂足为A2,交y轴于点A3;过点A3作A3A4⊥A2A3,垂足为A3,交x轴于点A4;过点A4作A4A5⊥A3A4,垂足为A4,交y轴于点A5;…按此规律进行下去,则点A2017的坐标为(0,31008).
如图,点A1的坐标为(0,1),A2在x轴的负半轴上,且∠A1A2O=30°,过点A2作A2A3⊥A1A2,垂足为A2,交y轴于点A3;过点A3作A3A4⊥A2A3,垂足为A3,交x轴于点A4;过点A4作A4A5⊥A3A4,垂足为A4,交y轴于点A5;…按此规律进行下去,则点A2017的坐标为(0,31008).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
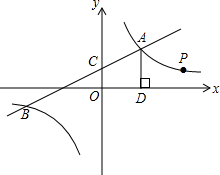 如图,一次函数y1=k1x+b与反比例函数y2=$\frac{{k}_{2}}{x}$的图象交于点A(4,m)和B(-8,-2),与y轴交于点C.
如图,一次函数y1=k1x+b与反比例函数y2=$\frac{{k}_{2}}{x}$的图象交于点A(4,m)和B(-8,-2),与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
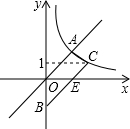 如图,梯形AOBC的顶点A,C在反比例函数图象上,OA∥BC,上底边OA在直线y=x上,下底边BC交y轴于B(0,-4),则四边形AOBC的面积为2$\sqrt{5}$+10.
如图,梯形AOBC的顶点A,C在反比例函数图象上,OA∥BC,上底边OA在直线y=x上,下底边BC交y轴于B(0,-4),则四边形AOBC的面积为2$\sqrt{5}$+10.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com