
【题目】如图,已知抛物线y=ax2﹣2ax﹣3a(a<0)与x轴交于A,B两点,点A在点B的左边,与y轴交于点C,顶点为D,若以BD为直径的⊙M经过点C.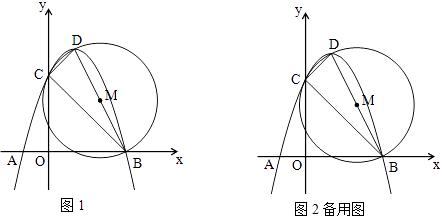
(1)请直接写出C,D两点的坐标(用含a的代数式表示);
(2)求抛物线的函数表达式;
(3)在抛物线上是否存在点E,使∠EDB=∠CBD?若存在,请求出所有满足条件的点E的坐标;若不存在,请说明理由.
【答案】
(1)
解:∵将x=0代入抛物线的解析式得y=﹣3a,
∴点C的坐标是(0,﹣3a).
∵x=﹣ ![]() =
= ![]() =1,
=1,
∴点D的横坐标为1.
∵将x=1代入抛物线的解析式得y=a﹣2a﹣3a=﹣4a,
∴点D的坐标是(1,﹣4a).
(2)
解:解:令y=0得:ax2﹣2ax﹣3a=0
∵a≠0,故得x1=﹣1,x2=3
∴A(﹣1,0),B(3,0).
如图1所示:过点D作DN⊥y轴于点N,则DN=1,CN=﹣4a﹣(﹣3a)=﹣a.
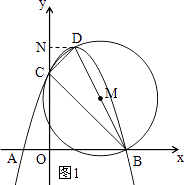
∵BD为⊙M的直径,
∴∠BCD=90°.
∴∠DCN+∠BCO=90°.
∵∠CDN+∠DCN=90°,
∴∠BCO=∠CDN,
∵∠BOC=∠DNC=90°,
∴△BOC∽△CND.
∴ ![]() ,即
,即 ![]() ,解得:a=±1(其中a=1舍去),
,解得:a=±1(其中a=1舍去),
∴a=﹣1.
∴所求抛物线为y=﹣x2+2x+3.
(3)
解:∵a=﹣1,
∴D(1,4).
∵设直线BC的解析式为y=kx+b,将B(3,0),C(0,3)代入得: ![]() ,解得:k=﹣1,b=3,
,解得:k=﹣1,b=3,
∴直线BC为:y=﹣x+3.
如图2所示:过点D作DE∥BC,交抛物线与点E.
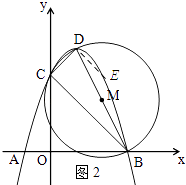
∵DE∥BC,
∴∠EDB=∠CBD.
∴设直线DE为y=﹣x+b
∵把点D(1,4)代入得:4=﹣1+b,解得:b=5,
∴直线DE为:y=﹣x+5.
解方程组 ![]() 得:
得: ![]() ,
, ![]()
∵D(1,4)
∴E(2,3).
如图3所示:作∠PDB=∠CBD,DP交BC于点P,交抛物线与点E.
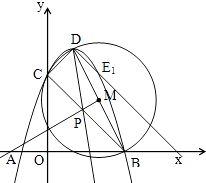
∵∠EDB=∠CBD,
∴PD=PB.
又∵MB=MD,
∴PM⊥BD.
∵B(3,0),D(1,4),
∴直线BD为y=﹣2x+6,且M(2,2)
∴设直线PM为 ![]() ,
,
∴2=1+b2,
∴b2=1
∴直线PM为: ![]()
解方程组 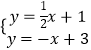 得:
得: ![]() ,
,
∴P( ![]() ,
, ![]() )
)
∵D(1,4),P( ![]() ,
, ![]() )
)
∴直线PD为:y=﹣7x+11
解方程组 ![]() 得:
得: ![]() ,
, ![]()
∵D(1,4),
∴E(8,﹣45).
综上所述,在抛物线上存在满足条件的点E,点E的坐标为E(2,3)或E(8,﹣45).
【解析】(1)将x=0代入抛物线的解析式可得到点C的坐标,依据抛物线的对称轴方程可求得点D的横坐标,然后将点D的横坐标代入可求得点D的纵坐标;(2)令y=0可求得点A、B的坐标,过点D作DN⊥y轴于点N,则DN=1,CN=﹣a.接下来证明△BOC∽△CND,然后依据相似三角形的性质可求得a的值,从而得到抛物线的解析式;(3)先求得点D的坐标、直线BC的解析式,点D作DE∥BC,交抛物线与点E.设直线DE的解析式为y=﹣x+b,把点D(1,4)代入直线DE的解析式求得b的值,然后将DE的解析式与抛物线的解析式组成方程可求得点E的坐标;作∠PDB=∠CBD,DP交BC于点P,交抛物线与点E.克证明MP垂直平分BD,从而可求得PM的解析式,然后由PM的解析式和BC的解析式可求得点P的坐标,接下来求得PD的解析式,最后根据DP的解析式和抛物线的解析式可求得E的坐标.
【考点精析】掌握二次函数的概念和二次函数的图象是解答本题的根本,需要知道一般地,自变量x和因变量y之间存在如下关系:一般式:y=ax2+bx+c(a≠0,a、b、c为常数),则称y为x的二次函数;二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,以直角三角形AOC的直角顶点O为原点,以OC、OA所在直线为x轴和y轴建立平面直角坐标系,点![]() ,
,![]() 满足
满足![]() .
.
![]() 则C点的坐标为______;A点的坐标为______.
则C点的坐标为______;A点的坐标为______.
![]() 已知坐标轴上有两动点P、Q同时出发,P点从C点出发沿x轴负方向以1个单位长度每秒的速度匀速移动,Q点从O点出发以2个单位长度每秒的速度沿y轴正方向移动,点Q到达A点整个运动随之结束
已知坐标轴上有两动点P、Q同时出发,P点从C点出发沿x轴负方向以1个单位长度每秒的速度匀速移动,Q点从O点出发以2个单位长度每秒的速度沿y轴正方向移动,点Q到达A点整个运动随之结束![]() 的中点D的坐标是
的中点D的坐标是![]() ,设运动时间为
,设运动时间为![]() 秒
秒![]() 问:是否存在这样的t,使
问:是否存在这样的t,使![]() ?若存在,请求出t的值;若不存在,请说明理由.
?若存在,请求出t的值;若不存在,请说明理由.
![]() 点F是线段AC上一点,满足
点F是线段AC上一点,满足![]() ,点G是第二象限中一点,连OG,使得
,点G是第二象限中一点,连OG,使得![]() 点E是线段OA上一动点,连CE交OF于点H,当点E在线段OA上运动的过程中,
点E是线段OA上一动点,连CE交OF于点H,当点E在线段OA上运动的过程中,![]() 的值是否会发生变化?若不变,请求出它的值;若变化,请说明理由.
的值是否会发生变化?若不变,请求出它的值;若变化,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知任意三角形的三边长,如何求三角形面积?
古希腊的几何学家海伦解决了这个问题,在他的著作《度量论》一书中给出了计算公式﹣﹣海伦公式S= ![]() (其中a,b,c是三角形的三边长,p=
(其中a,b,c是三角形的三边长,p= ![]() ,S为三角形的面积),并给出了证明
,S为三角形的面积),并给出了证明
例如:在△ABC中,a=3,b=4,c=5,那么它的面积可以这样计算:
∵a=3,b=4,c=5
∴p= ![]() =6
=6
∴S= ![]() =
= ![]() =6
=6
事实上,对于已知三角形的三边长求三角形面积的问题,还可用我国南宋时期数学家秦九韶提出的秦九韶公式等方法解决.
如图,在△ABC中,BC=5,AC=6,AB=9
(1)用海伦公式求△ABC的面积;
(2)求△ABC的内切圆半径r.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:EF∥AD ,∠1=∠2,∠BAC=70°,将求∠AGD的过程填写完整:

因为EF∥AD,所以∠2=__
又因为∠1=∠2,所以∠1=∠3
所以AB∥__
所以∠BAC+__=180°
因为∠BAC=70°,所以∠AGD=__
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC和△ECD都是等边三角形,B、C、D在一条直线上。
求证:(1)BE=AD;
(2) △FCH是等边三角形
(3)求∠EMD的度数。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F,将△DEF沿EF折叠,点D恰好落在BE上M点处,延长BC、EF交于点N.有下列四个结论:①DF=CF;②BF⊥EN;③△BEN是等边三角形;④S△BEF=3S△DEF.其中,将正确结论的序号全部选对的是( )

A. ①②③
B. ①②④
C. ②③④
D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)求证:四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D、E分别在边AB、AC上,DE∥BC,F为BC边上一点,连接AF交DE于点G,下列说法不正确的是( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学积极开展“阳光体育”活动,共开设了跳绳、乒乓球、篮球、跑步四种运动项目.为了解学生最喜爱哪一种项目,随机抽取了部分学生进行调查,并绘制了如下的条形统计图和扇形统计图(部分信息未给出)
(1)求本次被调查的学生人数;
(2)补全条形统计图;
(3)根据统计的数据估计该中学3200名学生中最喜爱篮球的人数约有_____人.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com