
【题目】如图,在平面直角坐标系中,直线![]() 与坐标轴分别交于
与坐标轴分别交于![]() ,
,![]() 两点,以线段
两点,以线段![]() 为边,在第一象限内作正方形
为边,在第一象限内作正方形![]() ,将正方形
,将正方形![]() 沿
沿![]() 轴负方向,平移
轴负方向,平移![]() 个单位长度,使点
个单位长度,使点![]() 恰好落在直线
恰好落在直线![]() 上,则
上,则![]() 的值为________.
的值为________.

【答案】1
【解析】
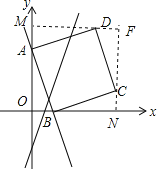
如图,作CN⊥OB于N,DM⊥OA于M,利用三角形全等,求出点D坐标即可解决问题.
解:如图作CN⊥OB于N,DM⊥OA于M,CN与DM交于点F,
∵直线y=-3x+3与x轴、y轴分别交于B、A两点,
∴点A(0,3),点B(1,0),
∵四边形ABCD是正方形,
∴AB=AD=DC=BC,∠ABC=90°,
∵∠BAO+∠ABO=90°,∠ABO+∠CBN=90°,
∴∠BAO=∠CBN,
在△BAO和△CBN中,
 ,
,
∴△BAO≌△CBN(AAS),
∴BN=AO=3,CN=BO=1,
同理可以得到:DF=AM=BO=1,CF=DM=AO=3,
∴点F(4,4),D(3,4),
∵将正方形ABCD沿x轴负方向平移a个单位长度,使点D恰好落在直线y=3x-2上,
∴把y=4代入y=3x-2得,x=2,
∴a=3-2=1,
∴正方形沿x轴负方向平移a个单位长度后,点D恰好落在直线y=3x-2上时,a=1,
故答案为1.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,点P在对角线AC上,且PA=PD,⊙O是△PAD的外接圆. 
(1)求证:AB是⊙O的切线;
(2)若AC=8,tan∠BAC= ![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,正确的个数是 ( )
①若三条线段的比为1:1:![]() ,则它们组成一个等腰直角三角形;②两条对角线相等的平行四边形是矩形;③对角线互相垂直的四边形是菱形;④有两个角相等的梯形是等腰梯形;⑤一条直线与矩形的一组对边相交,必分矩形为两个直角梯形。
,则它们组成一个等腰直角三角形;②两条对角线相等的平行四边形是矩形;③对角线互相垂直的四边形是菱形;④有两个角相等的梯形是等腰梯形;⑤一条直线与矩形的一组对边相交,必分矩形为两个直角梯形。
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E在以AB为直径的⊙O上,点C是 ![]() 的中点,过点C作CD垂直于AE,交AE的延长线于点D,连接BE交AC于点F.
的中点,过点C作CD垂直于AE,交AE的延长线于点D,连接BE交AC于点F. 
(1)求证:CD是⊙O的切线;
(2)若cos∠CAD= ![]() ,BF=15,求AC的长.
,BF=15,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与直线
与直线![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 是抛物线上
是抛物线上![]() ,
,![]() 之间的一个动点,过点
之间的一个动点,过点![]() 分别作
分别作![]() 轴、
轴、![]() 轴的平行线与直线
轴的平行线与直线![]() 交于点
交于点![]() ,
,![]() .
.

(1)求抛物线的解析式;
(2)若![]() 为
为![]() 的中点,求
的中点,求![]() 的长;
的长;
(3)如图,以![]() ,
,![]() 为边构造矩形
为边构造矩形![]() ,设点
,设点![]() 的坐标为
的坐标为![]() ,
,
①请求出![]() ,
,![]() 之间的关系式;②求出矩形
之间的关系式;②求出矩形![]() 的周长最大时,点
的周长最大时,点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC, EF∥BC,∠AEF=143°,AB=AE=1.3米,那么适合该地下车库的车辆限高标志牌为多少米?(结果精确到0.1.参考数据:sin 37° ≈ 0.60,cos 37° ≈ 0.80,tan 37° ≈ 0.75)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com