
分析 (1)方程组利用加减消元法求出解即可;
(2)方程组整理后,利用加减消元法求出解即可;
(3)方程组整理后,利用加减消元法求出解即可.
解答 解:(1)$\left\{\begin{array}{l}{2x+y=3①}\\{x-y=0②}\end{array}\right.$,
①+②得:3x=3,即x=1,
把x=1代入②得:y=1,
则方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$;
(2)方程组整理得:$\left\{\begin{array}{l}{2x-3y=6①}\\{3x+2y=22②}\end{array}\right.$,
①×2+②×3得:13x=78,即x=6,
把x=6代入①得:y=2,
则方程组的解为$\left\{\begin{array}{l}{x=6}\\{y=2}\end{array}\right.$;
(3)方程组整理得:$\left\{\begin{array}{l}{5x-11y=-1①}\\{-x+5y=3②}\end{array}\right.$,
①+②×5得:14y=14,即y=1,
把y=1代入②得:x=2,
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
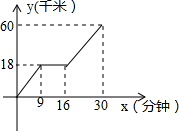 如图,是某汽车行驶的路程y(千米)与时间x(分钟)的函数关系图象,观察图中所提供的信息,解答下列问题.
如图,是某汽车行驶的路程y(千米)与时间x(分钟)的函数关系图象,观察图中所提供的信息,解答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,四边形OABC是矩形,点A、C的坐标分别为(6,0),(0,2),点D是线段BC上的动点(与端点B、C不重合),过点D作直线y=-x+b交折线OAB于点E.
如图所示,四边形OABC是矩形,点A、C的坐标分别为(6,0),(0,2),点D是线段BC上的动点(与端点B、C不重合),过点D作直线y=-x+b交折线OAB于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com