
 ��ͼ����ƽ��ֱ������ϵxOy�У���ֱ֪��AB��y=$\frac{2}{3}$x+4��x���ڵ�A����y���ڵ�B��ֱ��CD��y=-$\frac{1}{3}$x-1��ֱ��AB�ཻ�ڵ�M����x���ڵ�C����y���ڵ�D��
��ͼ����ƽ��ֱ������ϵxOy�У���ֱ֪��AB��y=$\frac{2}{3}$x+4��x���ڵ�A����y���ڵ�B��ֱ��CD��y=-$\frac{1}{3}$x-1��ֱ��AB�ཻ�ڵ�M����x���ڵ�C����y���ڵ�D������ ��1������y���ϵĵ�������������ɵó����ۣ�
��2���������M�����꣬���������ε����֮�ͼ��ɵó����ۣ�
��3��������������öԽ�����ƽ�ֵ��ı�����ƽ���ı��κ��߶ε��е������ȷ���������ɵó����ۣ�
��� �⣺��1���ߵ�B��ֱ��AB��y=$\frac{2}{3}$x+4��y��Ľ������꣬
��B��0��4����
�ߵ�D��ֱ��CD��y=-$\frac{1}{3}$x-1��y��Ľ������꣬
��D��0��-1����
��2����ͼ1��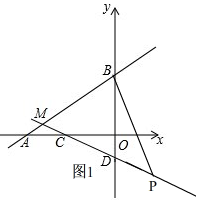 ��ֱ��AB��CD�ཻ��M��
��ֱ��AB��CD�ཻ��M��
��M��-5��$\frac{2}{3}$����
�ߵ�P�ĺ�����Ϊx��
���P��x��-$\frac{1}{3}$x-1����
��B��0��4����D��0��-1����
��BD=5��
�ߵ�P������MD�ϣ�����x��0ʱ��
S=S��BDM+S��BDP=$\frac{1}{2}$��5��5+x��=$\frac{5}{2}$x+$\frac{25}{2}$��
��3����ͼ��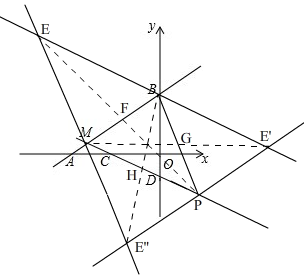 �ɣ�1��֪��S=$\frac{5}{2}$x+$\frac{25}{2}$��
�ɣ�1��֪��S=$\frac{5}{2}$x+$\frac{25}{2}$��
��S=20ʱ��$\frac{5}{2}$x+$\frac{25}{2}$=20��
��x=3��
��P��3��-2����
�ٵ�BP�ǶԽ���ʱ��ȡBP���е�G������MG���ӳ�ȡһ��E'ʹGE'=GE��
��E'��m��n����
��B��0��4����P��3��-2����
��BP���е�����Ϊ��$\frac{3}{2}$��1����
��M��-5��$\frac{2}{3}$����
��$\frac{-5+m}{2}$=$\frac{3}{2}$��$\frac{\frac{2}{3}+n}{2}$=1��
��m=8��n=$\frac{4}{3}$��
��E'��8��$\frac{4}{3}$����
�ڵ�ABΪ�Խ���ʱ��ͬ�ٵķ����ã�E��-9��6����
�۵�MPΪ�Խ���ʱ��ͬ�ٵķ����ã�E''��-2��-$\frac{16}{3}$����
�������������ĵ�E������Ϊ��8��$\frac{4}{3}$������-9��6������-2��-$\frac{16}{3}$����
���� ������һ�κ����ۺ��⣬��Ҫ�����������ε�����ļ��㷽����ƽ���ı��ε����ʣ��⣨2�����������ε�����ļ��㷽�����⣨3���Ĺؼ��Ƿ������۵�˼�������⣮


 ��������ϵ�д�
��������ϵ�д� ��ӡ�Ļ���ʱ����ϵ�д�
��ӡ�Ļ���ʱ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | am+bm-1=m��a+b��-1 | B�� | ��x+2����x-5��=x2-3x-10 | C�� | x2+5x+4=x��x+5+$\frac{4}{x}$�� | D�� | x2-4x=x��x-4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
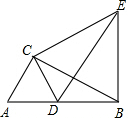
 ��ͼ��AC=BD��AD=BC����DBC=90�㣬̽��AD��AC��λ�ù�ϵ��˵�����ɣ�
��ͼ��AC=BD��AD=BC����DBC=90�㣬̽��AD��AC��λ�ù�ϵ��˵�����ɣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��Rt��ABC�У���ACB=90�㣬��ABC=30�㣬AC=1������ABC�Ƶ�C��ʱ����ת����CDE��ʹ�õ�Dǡ������AB�ϣ�����BE����BE�ij���Ϊ$\sqrt{3}$��
��ͼ��Rt��ABC�У���ACB=90�㣬��ABC=30�㣬AC=1������ABC�Ƶ�C��ʱ����ת����CDE��ʹ�õ�Dǡ������AB�ϣ�����BE����BE�ij���Ϊ$\sqrt{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
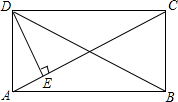 ��֪����ͼ���ھ���ABCD�У�DE��AC�ڵ�E����ADE����CDE=1��2����ô��BDC���ڣ�������
��֪����ͼ���ھ���ABCD�У�DE��AC�ڵ�E����ADE����CDE=1��2����ô��BDC���ڣ�������| A�� | 60�� | B�� | 45�� | C�� | 22.5�� | D�� | 30�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
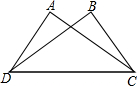
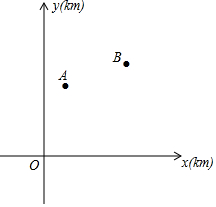 ��A��B������ׯ������ͼֽ�ϵ�����ֱ�Ϊ��2��5������7��7������ͼ��ʾ��x�����ڵ�λ��Ϊһ�����߹�·����Ҫ�ڹ�·����һ��������P��ʹ�÷�����P��������ׯA��B�ľ���֮����С��
��A��B������ׯ������ͼֽ�ϵ�����ֱ�Ϊ��2��5������7��7������ͼ��ʾ��x�����ڵ�λ��Ϊһ�����߹�·����Ҫ�ڹ�·����һ��������P��ʹ�÷�����P��������ׯA��B�ľ���֮����С���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com