
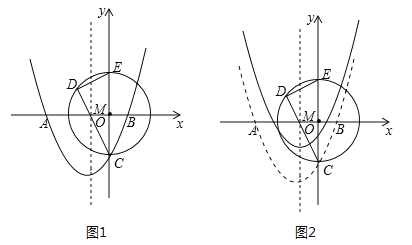
【题目】如图1,在平面直径坐标系中,抛物线![]() 与x轴交于点A(﹣3,0).B(1,0),与y轴交于点C.
与x轴交于点A(﹣3,0).B(1,0),与y轴交于点C.
(1)直接写出抛物线的函数解析式;
(2)以OC为半径的⊙O与y轴的正半轴交于点E,若弦CD过AB的中点M,试求出DC的长;
(3)将抛物线向上平移![]() 个单位长度(如图2)若动点P(x,y)在平移后的抛物线上,且点P在第三象限,请求出△PDE的面积关于x的函数关系式,并写出△PDE面积的最大值.
个单位长度(如图2)若动点P(x,y)在平移后的抛物线上,且点P在第三象限,请求出△PDE的面积关于x的函数关系式,并写出△PDE面积的最大值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)S△PDE=
;(3)S△PDE=![]() (
(![]() <x<0),且△PDE面积的最大值为
<x<0),且△PDE面积的最大值为![]() .
.
【解析】(1)将点A(﹣3,0)、B(1,0)代入![]() 中,得:
中,得:![]() ,解得:
,解得:![]() ,∴抛物线的函数解析式为
,∴抛物线的函数解析式为![]() .
.
(2)令![]() 中x=0,则y=﹣2,∴C(0,﹣2),∴OC=2,CE=4.
中x=0,则y=﹣2,∴C(0,﹣2),∴OC=2,CE=4.
∵A(﹣3,0),B(1,0),点M为线段AB的中点,∴M(﹣1,0),∴CM=![]() =
=![]() .
.
∵CE为⊙O的直径,∴∠CDE=90°,∴△COM∽△CDE,∴![]() ,∴DC=
,∴DC=![]() .
.
(3)将抛物线向上平移![]() 个单位长度后的解析式为
个单位长度后的解析式为![]() =
=![]() ,令
,令![]() 中y=0,即
中y=0,即![]() ,解得:
,解得:![]() =
=![]() ,
,![]() =
=![]() .
.
∵点P在第三象限,∴![]() <x<0.
<x<0.
过点P作PP′⊥y轴于点P′,过点D作DD′⊥y轴于点D′,如图所示.
在Rt△CDE中,CD=![]() ,CE=4,∴DE=
,CE=4,∴DE=![]() =
=![]() ,sin∠DCE=
,sin∠DCE=![]() =
=![]() ,在Rt△CDD′中,CD=
,在Rt△CDD′中,CD=![]() ,∠CD′D=90°,∴DD′=CDsin∠DCE=
,∠CD′D=90°,∴DD′=CDsin∠DCE=![]() ,CD′=
,CD′=![]() =
=![]() ,OD′=CD′﹣OC=
,OD′=CD′﹣OC=![]() ,∴D(
,∴D(![]() ,
,![]() ),D′(0,
),D′(0,![]() ),∵P(x,
),∵P(x,![]() ),∴P′(0,
),∴P′(0,![]() ),∴S△PDE=S△DD′E+S梯形DD′P′P﹣S△EPP′=
),∴S△PDE=S△DD′E+S梯形DD′P′P﹣S△EPP′=![]() DD′ED′+
DD′ED′+![]() (DD′+PP′)D′P′﹣
(DD′+PP′)D′P′﹣![]() PP′EP′=
PP′EP′=![]() (
(![]() <x<0),∵S△PDE=
<x<0),∵S△PDE=![]() =
=![]() ,
,![]() <
<![]() <0,∴当x=
<0,∴当x=![]() 时,S△PDE取最大值,最大值为
时,S△PDE取最大值,最大值为![]() .
.
故:△PDE的面积关于x的函数关系式为S△PDE=![]() (
(![]() <x<0),且△PDE面积的最大值为
<x<0),且△PDE面积的最大值为![]() .
.



 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,点E是AB的中点,延长CB至D,使BD= ![]() BC.
BC. 
(1)用尺规作图的方法,过E点作EF⊥DC,垂足是点F;(不写作法,保留作图痕迹)
(2)求证:DF=CF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】线段AB的两个端点的坐标为A(m,2),B(3,5),将线段AB平移后得线段A′B′,其中A′(0,3),B′(6,n),则线段AB上的点C(-1,3)平移后的坐标是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,以AC为直径的⊙O与BC交于点D,DE⊥AB,垂足为E,ED的延长线与AC的延长线交于点F。

(1)求证:DE是⊙O的切线;
(2)若⊙O的半径为4,BE=2,求∠F的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平移的过程中,新图形中的每一点都是由原图形中的某一点移动后得到的,这两点是______,连接各组对应点的线段________.平移后的图形的位置是由平移的_____和平移的____决定的.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com