
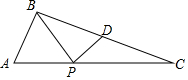
 如图,△ABC中,AB=$\sqrt{5}$,AC=5,tanA=2,D是BC中点,点P是AC上一个动点,将△BPD沿PD折叠,折叠后的三角形与△PBC的重合部分面积恰好等于△BPD面积的一半,则AP的长为2或5-$\sqrt{5}$.
如图,△ABC中,AB=$\sqrt{5}$,AC=5,tanA=2,D是BC中点,点P是AC上一个动点,将△BPD沿PD折叠,折叠后的三角形与△PBC的重合部分面积恰好等于△BPD面积的一半,则AP的长为2或5-$\sqrt{5}$. 分析 分两种情况:
①当点B′在AC的下方时,如图1,先根据中点的性质和重合部分面积恰好等于△BPD面积的一半得:F是PC的中点,由中位线得:DF∥BP,利用平行线的性质:得内错角相等,由折叠得角相等可得:∠B′PD=∠PDF,则PB=BD,利用tan∠A=$\frac{BE}{AE}$=2,计算AB=$\sqrt{5}$,从而得AP的长;
②当点B'在AC的上方时,如图2,连接B′C,证明四边形DPCB′是平行四边形,则PC=B′D=BD=$\sqrt{5}$,得AP的长.
解答 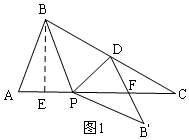 解:分两种情况:
解:分两种情况:
①当点B′在AC的下方时,如图1,
∵D是BC中点,
∴S△BPD=S△PDC,
∵S△PDF=$\frac{1}{2}$S△BPD,
∴S△PDF=$\frac{1}{2}$S△PDC,
∴F是PC的中点,
∴DF是△BPC的中位线,
∴DF∥BP,
∴∠BPD=∠PDF,
由折叠得:∠BPD=∠B′PD,
∴∠B′PD=∠PDF,
∴PB′=B′D,
即PB=BD,
过B作BE⊥AC于E,
Rt△ABE中,tan∠A=$\frac{BE}{AE}$=2,
∵AB=$\sqrt{5}$,
∴AE=1,BE=2,
∴EC=5-1=4,
由勾股定理得:BC=$\sqrt{B{E}^{2}+E{C}^{2}}$=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
∵D为BC的中点,
∴BD=$\sqrt{5}$,
∴PB=BD=$\sqrt{5}$,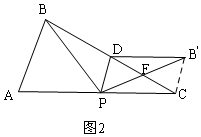
在Rt△BPE中,PE=1,
∴AP=AE+PE=1=1=2;
②当点B'在AC的上方时,如图2,连接B′C,
同理得:F是DC的中点,F是PB′的中点,
∴DF=FC,PF=FB′,
∴四边形DPCB′是平行四边形,
∴PC=B′D=BD=$\sqrt{5}$,
∴AP=5-$\sqrt{5}$,
综上所述,AP的长为2或5-$\sqrt{5}$;
故答案为:2或5-$\sqrt{5}$.
点评 本题考查了折叠变换问题、等积变换、三角形的中位线性质、平行线的性质、平行四边形的性质和判定以及勾股定理的综合运用,本题综合性较强,有一定的难度.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:选择题
| A. | 1.196×109 | B. | 1.196×108 | C. | 1.196×104 | D. | 11.96×108 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2013}{2016}$ | B. | $\frac{2015}{2016}$ | C. | $\frac{2015}{4032}$ | D. | $\frac{2017}{4032}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
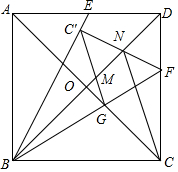 在正方形ABCD中,点E是AD的中点,连接BE,BF平分∠EBC交CD于点F,交AC于点G,将△CGF沿直线GF折叠至△C′GF,BD与△C′GF相交于点M、N,连接CN,若AB=6,则四边形CNC′G的面积是6-$\frac{6}{5}\sqrt{5}$.
在正方形ABCD中,点E是AD的中点,连接BE,BF平分∠EBC交CD于点F,交AC于点G,将△CGF沿直线GF折叠至△C′GF,BD与△C′GF相交于点M、N,连接CN,若AB=6,则四边形CNC′G的面积是6-$\frac{6}{5}\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ∠A=∠B=2∠C | B. | ∠A+∠B=∠C | C. | ∠A:∠B:∠C=1:4:5 | D. | ∠A=37°,∠B=53° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com