
【题目】在平面直角坐标系xOy中,已知点A,对点A作如下变换:
第一步:作点A关于x轴的对称点A1;第二步:以O为位似中心,作线段OA1的位似图形OA2,且相似比![]() =q,则称A2是点A的对称位似点.
=q,则称A2是点A的对称位似点.
(1)若A(2,3),q=2,直接写出点A的对称位似点的坐标;
(2)已知直线l:y=kx-2,抛物线C:y=-![]() x2+mx-2(m>0).点N(
x2+mx-2(m>0).点N(![]() ,2k-2)在直线l上.
,2k-2)在直线l上.
①当k=![]() 时,判断E(1,-1)是否是点N的对称位似点,请说明理由;
时,判断E(1,-1)是否是点N的对称位似点,请说明理由;
②若直线l与抛物线C交于点M(x1,y1)(x1≠0),且点M不是抛物线的顶点,则点M的对称位似点是否可能仍在抛物线C上?请说明理由.
【答案】(1)![]() 、
、![]() ;(2)①E(1,-1)不是N(2,-1)的对称位似点;②
;(2)①E(1,-1)不是N(2,-1)的对称位似点;②![]() .理由见解析.
.理由见解析.
【解析】
(1)由对称位似点的定义可求出点A的对称位似点的坐标;
(2)①先求出N点坐标为(2,1),关于x轴的对称点坐标为(2,1),由E(1,1),
![]() ,故不存在q,使得E(1,1)是点N的对称位似点,可知E(1,1)不是点N的对称位似点;
,故不存在q,使得E(1,1)是点N的对称位似点,可知E(1,1)不是点N的对称位似点;
②把N点坐标代入y=kx2,可得m=2k或m=k,当直线与二次函数图象相交时求得M(4k,4k22),![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,求出直线
,求出直线![]() 的解析式,联立方程组,当△≥0时,求得
的解析式,联立方程组,当△≥0时,求得![]() 时,点M的对称位似点仍在抛物线C上.
时,点M的对称位似点仍在抛物线C上.
解:(1)∵A(2,3),
∴A关于x轴的对称点A1为(2,3)),
∵以O为位似中心,作线段OA1的位似图形OA2,且相似比为2,
∴A2的坐标为(4,6)或(-4,6),
∴A的对称位似点的坐标为(4,6)或(4,6).
![]() 、
、![]()
(2)①当![]() 时,
时,![]() ,将
,将![]() 代入
代入![]() 得:
得:![]()
![]()
![]() 的坐标为
的坐标为![]() ,其关于
,其关于![]() 轴的对称点坐标是
轴的对称点坐标是![]()
对于![]() ,
,
![]() ,所构成的
,所构成的![]() 直角边不成比例,
直角边不成比例,
![]() 不是
不是![]() 的对称位似点
的对称位似点
②直线![]() :
:![]() 过点
过点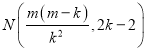
![]() ,整理得:
,整理得:![]()
![]()
![]() 或
或![]()
直线与抛物线相交于点![]() :
:![]()
![]()
![]() ,
,![]() ,
,![]()
抛物线对称轴:![]() ,且点
,且点![]() 不是抛物线的顶点
不是抛物线的顶点
![]() ,
,![]()
![]() 只有
只有![]() 成立. 此时,
成立. 此时,![]()
![]() 的坐标:
的坐标:![]()
于是,![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,
,
直线![]() 的解析式:
的解析式:![]()
若直线![]() 与抛物线有相交,
与抛物线有相交,![]()
整理得:![]()
当![]() ,
,![]() 时,交点存在,不妨设为
时,交点存在,不妨设为![]() ,
,![]() ,
,
则![]() 是点
是点![]() 的对称位似点
的对称位似点
![]() ,且
,且![]() ,
,
![]() ,
,
![]() .
.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:
【题目】抛物线y=﹣![]() x2﹣
x2﹣![]() x+
x+![]() 与x轴交于点A,B(点A在点B的左边),与y轴交于点C,点D是该抛物线的顶点.
与x轴交于点A,B(点A在点B的左边),与y轴交于点C,点D是该抛物线的顶点.
(1)如图1,连接CD,求线段CD的长;
(2)如图2,点P是直线AC上方抛物线上一点,PF⊥x轴于点F,PF与线段AC交于点E;将线段OB沿x轴左右平移,线段OB的对应线段是O1B1,当PE+![]() EC的值最大时,求四边形PO1B1C周长的最小值,并求出对应的点O1的坐标;
EC的值最大时,求四边形PO1B1C周长的最小值,并求出对应的点O1的坐标;
(3)如图3,点H是线段AB的中点,连接CH,将△OBC沿直线CH翻折至△O2B2C的位置,再将△O2B2C绕点B2旋转一周在旋转过程中,点O2,C的对应点分别是点O3,C1,直线O3C1分别与直线AC,x轴交于点M,N.那么,在△O2B2C的整个旋转过程中,是否存在恰当的位置,使△AMN是以MN为腰的等腰三角形?若存在,请直接写出所有符合条件的线段O2M的长;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .
.![]() 是边
是边![]() 的中点,点
的中点,点![]() 为边
为边![]() 上的一个动点(与点
上的一个动点(与点![]() 、
、![]() 不重合),过点
不重合),过点![]() 作
作![]() ,交边
,交边![]() 于点
于点![]() .联结
.联结![]() 、
、![]() ,设
,设![]() .
.
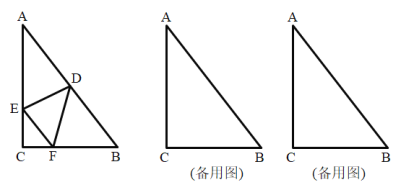
(1)当![]() 时,求
时,求![]() 的面积;
的面积;
(2)如果点![]() 关于
关于![]() 的对称点为
的对称点为![]() ,点
,点![]() 恰好落在边
恰好落在边![]() 上时,求
上时,求![]() 的值;
的值;
(3)以点![]() 为圆心,
为圆心,![]() 长为半径的圆与以点
长为半径的圆与以点![]() 为圆心,
为圆心,![]() 长为半径的圆相交,另一个交点
长为半径的圆相交,另一个交点![]() 恰好落在线段
恰好落在线段![]() 上,求
上,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2019年某中学举行的冬季阳径运动会上,参加男子跳高的15名运动员的成绩如表所示:
成绩(m) | 1.80 | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 |
人数 | 1 | 2 | 4 | 3 | 3 | 2 |
这些运动员跳高成绩的中位数和众数分别是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() .
.
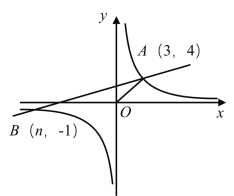
(1)求反比例函数和一次函数的解析式;
(2)在x轴上存在一点C,使![]() 为等腰三角形,求此时点C的坐标;
为等腰三角形,求此时点C的坐标;
(3)根据图象直接写出使一次函数的值大于反比例函数的值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
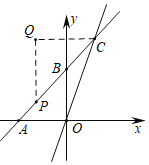
【题目】如图,在平面直角坐标系中,直线11:y=k1x+3分别与x轴,y轴交于A(﹣3,0),B两点,与直线l2:y=k2x交于点C,S△AOC=9.
(1)求tan∠BAO的值;
(2)求出直线l2的解析式;
(3)P为线段AC上一点(不含端点),连接OP,一动点H从点O出发,沿线段OP以每秒1个单位长度的速度运动到P,再沿线段PC以每秒![]() 个单位长度的速度运动到点C后停止,请直接写出点H在整个运动过程的最少用时.
个单位长度的速度运动到点C后停止,请直接写出点H在整个运动过程的最少用时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商业集团新建一小车停车场,经测算,此停车场每天需固定支出的费用(设施维修费、车辆管理人员工资等)为800元.为制定合理的收费标准,该集团对一段时间每天小车停放辆次与每辆次小车的收费情况进行了调查,发现每辆次小车的停车费不超过5元时,每天来此处停放的小车可达1440辆次;若停车费超过5元,则每超过1元,每天来此处停放的小车就减少120辆次.为便于结算,规定每辆次小车的停车费x(元)只取整数,用y(元)表示此停车场的日净收入,且要求日净收入不低于2512元.(日净收入=每天共收取的停车费﹣每天的固定支出)
(1)当x≤5时,写出y与x之间的关系式,并说明每辆小车的停车费最少不低于多少元;
(2)当x>5时,写出y与x之间的函数关系式(不必写出x的取值范围);
(3)该集团要求此停车场既要吸引客户,使每天小车停放的辆次较多,又要有较大的日净收入.按此要求,每辆次小车的停车费应定为多少元?此时日净收入是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种成本为每台20元的台灯,规定销售单价不低于成本价,又不高于每台32元.销售中平均每月销售量y(台)与销售单价x(元)的关系可以近似地看做一次函数,如下表所示:
x | 22 | 24 | 26 | 28 |
y | 90 | 80 | 70 | 60 |
(1)请直接写出y与x之间的函数关系式;
(2)为了实现平均每月375元的台灯销售利润,这种台灯的售价应定为多少?这时每月应购进台灯多少个?
(3)设超市每月台灯销售利润为ω(元),求ω与x之间的函数关系式,当x取何值时,ω的值最大?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知:函数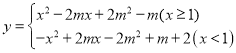 .
.
(1)当![]() 时,
时,
①求![]() 随
随![]() 增大而增大时,
增大而增大时,![]() 的取值范围;
的取值范围;
②当![]() 时,求
时,求![]() 的取值范围;
的取值范围;
③当![]() 时,设
时,设![]() 的最大值与最小值之差为
的最大值与最小值之差为![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
(2)若![]() ,连结
,连结![]() .当此函数的图象与线段
.当此函数的图象与线段![]() 只有两个公共点时,直接写出
只有两个公共点时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com