
ЁОЬтФПЁПФГЯчеђвЊдкЩњЛюРЌЛјДцЗХЧјНЈвЛИіРЯФъЛюЖЏжааФЃЌетбљБиаыАб1200СЂЗНУзЕФЩњЛюРЌЛјдЫзпЃК
ЃЈ1ЃЉМйШчУПЬьФмдЫxСЂЗНУзЃЌЫљашЪБМфЮЊyЬьЃЌаДГіyгыxжЎМфЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉШєУПСОЭЯРЛњвЛЬьФмдЫ12СЂЗНУзЃЌдђ5СОетбљЕФЭЯРЛњвЊгУЖрЩйЬьВХФмдЫЭъЃП
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЧщПіЯТЃЌдЫСЫ8ЬьКѓЃЌЪЃЯТЕФШЮЮёвЊдкВЛГЌЙ§6ЬьЕФЪБМфФкЭъГЩЃЌФЧУДжСЩйашвЊдіМгЖрЩйСОетбљЕФЭЯРЛњВХФмАДЪБЭъГЩШЮЮёЃП
ЁОД№АИЁП(1)![]() Ьь(2)вЊ20ЬьВХФмЭъГЩЃЛ(3)жСЩйашвЊдіМг5СОЃЎ
Ьь(2)вЊ20ЬьВХФмЭъГЩЃЛ(3)жСЩйашвЊдіМг5СОЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉИљОнУПЬьФмдЫxm3ЃЌЫљашЪБМфЮЊyЬьЕФЛ§ОЭЪЧ1200m3ЃЌМДПЩаДГіКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉАбx=12ЁС5=60ДњШыЃЌМДПЩЧѓЕУЬьЪ§ЃЛ
ЃЈ3ЃЉЪзЯШЫуГі8ЬьвдКѓЪЃгрЕФЪ§СПЃЌШЛКѓМЦЫуГі6ЬьдЫЭъЫљашЕФЭЯРЛњЪ§ЃЌМДПЩЧѓНтЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉЁпxy=1200ЃЌ
Ёрy=![]() ЃЛ
ЃЛ
ЃЈ2ЃЉx=12ЁС5=60ЃЌДњШыКЏЪ§НтЮіЪНЕУЃЛy=![]() =20ЃЈЬьЃЉ
=20ЃЈЬьЃЉ
Д№ЃК20ЬьдЫЭъЃЛ
ЃЈ3ЃЉдЫСЫ8ЬьКѓЪЃгрЕФРЌЛјЪЧ1200-8ЁС60=720m3ЃЎ
ЪЃЯТЕФШЮЮёвЊдкВЛГЌЙ§6ЬьЕФЪБМфЭъГЩдђУПЬьжСЩйдЫ720ЁТ6=120m3ЃЌ
дђашвЊЕФЭЯРЛњЪ§ЪЧЃК120ЁТ12=10ЃЈСОЃЉЃЌ
дђжСЩйашвЊдіМг10-5=5СОетбљЕФЭЯРЛњВХФмАДЪБЭъГЩШЮЮёЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊвЛДЮКЏЪ§yЃНЉx+mКЭyЃН2x+nЕФЭМЯѓЖМОЙ§AЃЈЉ4ЃЌ0ЃЉЃЌЧвгыyжсЗжБ№НЛгкBЁЂCСНЕуЃЌдђЁїABCЕФУцЛ§ЮЊЃЈЁЁЁЁЃЉ
A.48B.36C.24D.18
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯC=90ЁуЃЌЁЯBACЕФЦНЗжЯпНЛBCгкЕуDЃЌЕуOдкABЩЯЃЌвдЕуOЮЊдВаФЃЌOAЮЊАыОЖЕФдВЧЁКУОЙ§ЕуDЃЌЗжБ№НЛACЃЌABгкЕуEЃЌFЃЎ
ЃЈ1ЃЉЪдХаЖЯжБЯпBCгыЁбOЕФЮЛжУЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉШєBD=2![]() ЃЌBF=2ЃЌЧѓвѕгАВПЗжЕФУцЛ§ЃЈНсЙћБЃСєІаЃЉЃЎ
ЃЌBF=2ЃЌЧѓвѕгАВПЗжЕФУцЛ§ЃЈНсЙћБЃСєІаЃЉЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
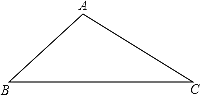
ЁОЬтФПЁПЯТУцЪЧаЁЖЋЩшМЦЕФЁАзїЁїABCжаBCБпЩЯЕФИпЯпЁБЕФГпЙцзїЭМЙ§ГЬЃЎ
вбжЊЃКЁїABCЃЎ
ЧѓзїЃКЁїABCжаBCБпЩЯЕФИпЯпADЃЎ
зїЗЈЃКШчЭМЃЌ
ЂйвдЕуBЮЊдВаФЃЌBAЕФГЄЮЊАыОЖзїЛЁЃЌвдЕуCЮЊдВаФЃЌCAЕФГЄЮЊАыОЖзїЛЁЃЌСНЛЁдкBCЯТЗННЛгкЕуEЃЛ
ЂкСЌНгAEНЛBCгкЕуDЃЎ
ЫљвдЯпЖЮADЪЧЁїABCжаBCБпЩЯЕФИпЯпЃЎ
ИљОнаЁЖЋЩшМЦЕФГпЙцзїЭМЙ§ГЬЃЌ
ЃЈ1ЃЉЪЙгУжБГпКЭдВЙцЃЌВЙШЋЭМаЮЃЛЃЈБЃСєзїЭМКлМЃЃЉ
ЃЈ2ЃЉЭъГЩЯТУцЕФжЄУїЃЎ
жЄУїЃКЁп =BAЃЌ =CAЃЌ
ЁрЕуBЃЌCЗжБ№дкЯпЖЮAEЕФДЙжБЦНЗжЯпЩЯЃЈ ЃЉЃЈЬюЭЦРэЕФвРОнЃЉЃЎ
ЁрBCДЙжБЦНЗжЯпЖЮAEЃЎ
ЁрЯпЖЮADЪЧЁїABCжаBCБпЩЯЕФИпЯпЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
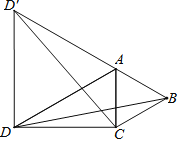
ЁОЬтФПЁПШчЭМЃЌдкЁїACDжаЃЌAD=9ЃЌCD=![]() ,ЁїABCжаЃЌAB=ACЃЌШєЁЯCAB=60Ёу,ЁЯADC=30Ёу,дкЁїACDЭтзїЕШБпЁїADDЁф
,ЁїABCжаЃЌAB=ACЃЌШєЁЯCAB=60Ёу,ЁЯADC=30Ёу,дкЁїACDЭтзїЕШБпЁїADDЁф
ЃЈ1ЃЉЧѓжЄЃКBD=CDЁф
ЃЈ2ЃЉЧѓBDЕФГЄ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПжабыЕчЪгЬЈЕФЁЖРЪЖСепЁЗНкФПМЄЗЂСЫЭЌбЇУЧЕФЖСЪщШШЧщЃЌЮЊСЫв§ЕМбЇЩњЁАЖрЖСЪщЃЌЖСКУЪщЁБЃЌФГаЃЖдАЫФъМЖВПЗжбЇЩњЕФПЮЭтдФЖССПНјааСЫЫцЛњЕїВщЃЌећРэЕїВщНсЙћЗЂЯжЃЌбЇЩњПЮЭтдФЖСЕФБОЪ§СПЩйЕФга![]() БОЃЌзюЖрЕФга
БОЃЌзюЖрЕФга![]() БОЃЌВЂИљОнЕїВщНсЙћЛцжЦСЫВЛЭъећЕФЭМБэЃЌШчЯТЫљЪОЃК
БОЃЌВЂИљОнЕїВщНсЙћЛцжЦСЫВЛЭъећЕФЭМБэЃЌШчЯТЫљЪОЃК
БОЪ§ЃЈБОЃЉ | ЦЕЪ§ЃЈШЫЪ§ЃЉ | ЦЕТЪ |
|
|
|
|
|
|
|
|
|
|
|
|
КЯМЦ |
|
|

ЃЈ![]() ЃЉЭГМЦЭМБэжаЕФ
ЃЉЭГМЦЭМБэжаЕФ![]() __________ЃЌ
__________ЃЌ![]() __________ЃЌ
__________ЃЌ![]() __________ЃЎ
__________ЃЎ
ЃЈ![]() ЃЉЧыНЋЦЕЪ§ЗжВМжБЗНЭМВЙГфЭъећЃЎ
ЃЉЧыНЋЦЕЪ§ЗжВМжБЗНЭМВЙГфЭъећЃЎ
ЃЈ![]() ЃЉЧѓЫљгаБЛЕїВщбЇЩњПЮЭтдФЖСЕФЦНОљБОЪ§ЃЎ
ЃЉЧѓЫљгаБЛЕїВщбЇЩњПЮЭтдФЖСЕФЦНОљБОЪ§ЃЎ
ЃЈ![]() ЃЉШєИУаЃАЫФъМЖЙВга
ЃЉШєИУаЃАЫФъМЖЙВга![]() УћбЇЩњЃЌЧыФуЙРМЦИУаЃАЫФъМЖбЇЩњПЮЭтдФЖС
УћбЇЩњЃЌЧыФуЙРМЦИУаЃАЫФъМЖбЇЩњПЮЭтдФЖС![]() БОМАвдЩЯЕФШЫЪ§ЃЎ
БОМАвдЩЯЕФШЫЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
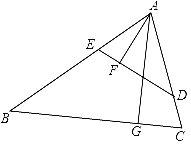
ЁОЬтФПЁПШчЭМЃЌдкШёНЧШ§НЧаЮABCжаЃЌЕуDЃЌEЗжБ№дкБпACЃЌABЩЯЃЌAGЁЭBCгкЕуGЃЌAFЁЭDEгкЕуFЃЌЁЯEAF=ЁЯGACЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїADEЁзЁїABCЃЛ
ЃЈ2ЃЉШєAD=3ЃЌAB=5ЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
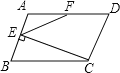
ЁОЬтФПЁПШчЭМдкЁѕABCDжаЃЌBC=2ABЃЌCEЁЭABгкEЃЌFЮЊADЕФжаЕуЃЌШєЁЯAEF=52ЁуЃЌдђЁЯB=___.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈЮЪЬтЧщОГЃЉ
ШчЭМ1ЃЌЫФБпаЮABCDЪЧе§ЗНаЮЃЌMЪЧBCБпЩЯЕФвЛЕуЃЌEЪЧCDБпЕФжаЕуЃЌAEЦНЗжЁЯDAMЃЎ
ЃЈЬНОПеЙЪОЃЉ
(1)жЄУїЃКAM=AD+MCЃЛ
(2)AM=DE+BMЪЧЗёГЩСЂЃПШєГЩСЂЃЌЧыИјГіжЄУїЃЛШєВЛГЩСЂЃЌЧыЫЕУїРэгЩЃЎ
ЃЈЭиеЙбгЩьЃЉ
(3)ШєЫФБпаЮABCDЪЧГЄгыПэВЛЯрЕШЕФОиаЮЃЌЦфЫћЬѕМўВЛБфЃЌШчЭМ2ЃЌЬНОПеЙЪО(1)ЁЂ(2)жаЕФНсТлЪЧЗёГЩСЂЃПЧыЗжБ№зїГіХаЖЯЃЌВЛашвЊжЄУїЃЎ

ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com