
【题目】如图,这条花边中有4个圆和4个正三角形,且这条花边的总长度![]() 为4,则花边上正三角形的内切圆半径为()
为4,则花边上正三角形的内切圆半径为()

A.![]() B.
B.![]() C.1D.
C.1D.![]()
【答案】A
【解析】
画出图形,连接AD,OH,则AD过O,求出∠OHC=30°,求出DH,根据勾股定理即可求出内切圆半径OD.
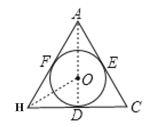
解:从中选择一个等边三角形和其内接圆如图,⊙O是△AHC的内切圆,⊙O切AH于F,切AC于E,切HC于D,
连接AD,OH,则AD过O(因为等边三角形的内切圆的圆心再角平分线上,也在底边的垂直平分线上),
∵△AHC是等边三角形,
∴∠AHC=60°,
∵⊙O是△AHC的内切圆,
∴∠OHC=![]() ∠AHC=30°,
∠AHC=30°,
∵HC=![]() AB=2,
AB=2,
∴HD=1,AH=2,
∴AD=![]() ,
,
在直角三角形OHD中,由勾股定理得:OD2+HD2=OH2 ,
得出:OD2+ 12 =(![]() -OD)2,
-OD)2,
∴OD=![]() (cm),
(cm),
故答案为:A


科目:初中数学 来源: 题型:
【题目】如图1,矩形ABCD中,AD=2,AB=a,点E为AD的中点,连接BE.过BE的中点F作FG⊥BE,交射线BC于点G,交边CD于H点.
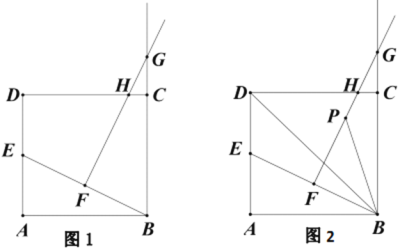
(1)连接HE、HB
①求证:HE=HB;
②若a=4,求CH的长.
(2)连接EG,△BEG面积为S
①BE= (用含a的代数式表示);
②求S与a的函数关系式.
(3)如图2,设FG的中点为P,连接PB、BD.猜想∠GBP与∠DBE的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿BC边上的中线AD平移到△A'B'C'的位置,已知△ABC的面积为9,阴影部分三角形的面积为4.若AA'=1,则A'D等于( )

A. 2 B. 3 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的方程![]() 有两个不相等的实数根.
有两个不相等的实数根.
(1)求m的取值范围;
(2)是否存在实数m,使方程的两个实数根的倒数和等于0?若存在,求出m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司销售部有营业员![]() 人,某一月的销售量统计如下表所示:
人,某一月的销售量统计如下表所示:
公司![]() 名营业员某一月的销售量统计表
名营业员某一月的销售量统计表
月销售量/件数 | 1770 | 480 | 220 | 180 | 120 | 90 |
人数 | 1 | 1 | 3 | 3 | 3 | 4 |
(1)求这![]() 名营业员该月销售量数据的平均数;
名营业员该月销售量数据的平均数;
(2)这![]() 名营业员该月销售量数据的中位数是 件,众数是 件,为了提高大多数营业员的积极性,实行“每天定额售量,超出有奖”的措施.如果你是管理者,你选择.确定“定额”的统计量为 (填“中位数”或“众数”)
名营业员该月销售量数据的中位数是 件,众数是 件,为了提高大多数营业员的积极性,实行“每天定额售量,超出有奖”的措施.如果你是管理者,你选择.确定“定额”的统计量为 (填“中位数”或“众数”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电工想换房间的灯泡,已知灯泡到地面的距离为![]() ,现有一架家用可调节式脚踏人字梯,其中踏板、地面都是水平的.梯子的侧面简化结构如图所示,左右支撑架长度相等,
,现有一架家用可调节式脚踏人字梯,其中踏板、地面都是水平的.梯子的侧面简化结构如图所示,左右支撑架长度相等,![]() .设梯子一边
.设梯子一边![]() 与地面的夹角为
与地面的夹角为![]() ,且
,且![]() 可调节的范围为
可调节的范围为![]() .当
.当![]() 时,电工站在梯子安全挡中最高一档踏板
时,电工站在梯子安全挡中最高一档踏板![]() 上的最大触及高度为
上的最大触及高度为![]() .
.
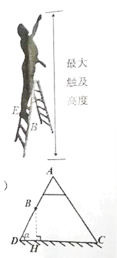
(1)当![]() 时,求踏板
时,求踏板![]() 离地面的高度
离地面的高度![]() .(精确到
.(精确到![]() )
)
(2)调节角度,试判断电工是否可以换下灯泡,并说明理由.(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
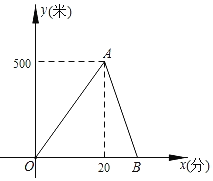
【题目】某湖边健身步道全长1500米,甲、乙两人同时从同一起点匀速向终点步行.甲先到达终点后立刻返回,在整个步行过程中,甲、乙两人间的距离y(米)与出发的时间x(分)之间的关系如图中OA﹣AB折线所示.
(1)用文字语言描述点A的实际意义;
(2)求甲、乙两人的速度及两人相遇时x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E是AD上的一个动点,连接BE,作点A关于BE的对称点F,且点F落在矩形ABCD的内部,连接AF,BF,EF,过点F作GF⊥AF交AD于点G,设![]() .
.
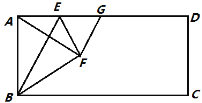
(1)求证:AE=GE;
(2)当点F落在AC上时,用含n的代数式表示![]() 的值;
的值;
(3)若AD=4AB,且以点F,C,G为顶点的三角形是直角三角形,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
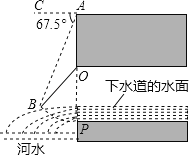
【题目】如图所示是我国古代城市用以滞洪或分洪系统的局部截面原理图,图中OP为下水管道口直径,OB为可绕转轴O自由转动的阀门.平时阀门被管道中排出的水冲开,可排出城市污水;当河水上涨时,阀门会因河水压迫而关闭,以防河水倒灌入城中.若阀门的直径OB=OP=100cm,OA为检修时阀门开启的位置,且OA=OB.
(1)直接写出阀门被下水道的水冲开与被河水关闭过程中∠POB的取值范围;
(2)为了观测水位,当下水道的水冲开阀门到达OB位置时,在点A处测得俯角∠CAB=67.5°,若此时点B恰好与下水道的水平面齐平,求此时下水道内水的深度.(结果保留小数点后一位)
(![]() =1.41,sin67.5°=0.92,cos67.5°=0.38,tan67.5°=2.41,sin22.5°=0.38,cos22.5°=0.92,tan22.5°=0.41)
=1.41,sin67.5°=0.92,cos67.5°=0.38,tan67.5°=2.41,sin22.5°=0.38,cos22.5°=0.92,tan22.5°=0.41)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com