

分析 问题拓展:直接根据圆的定义即可得出结论;
综合应用:①先判断出△POB≌△PAB,即可得出结论;
②先得出点Q是BP中点,再根据含30°角的直角三角形的性质确定出点B的坐标,进而得出点Q的坐标,
解答 解:问题拓展:根据圆的定义得,(x-a)2+(y-b)2=r2,
故答案为:(x-a)2+(y-b)2=r2,
综合应用:①∵PO=PA PD⊥OA,
∴∠OPD=∠APD,
在△POB和△PAB中 $\left\{\begin{array}{l}{PO=PA}\\{∠OPB=∠APB}\\{PB=PB}\end{array}\right.$,
∴△POB≌△PAB,
∴∠PAB=∠POB=90°,
∴PA⊥AB
∴AB是⊙P的切线,
②存在到四点O,P,A,B距离都相等的点Q,
当点Q在线段BP中点时
∵∠POB=∠PAB=90°,
∴QO=QP=QA=QB
∴此时点Q到四点O,P,A,B距离都相等
∵PB⊥OA,∠POB=90°,∠POA=30°
∴∠PBO=30°.
∴在Rt△POB中,OP=6,
∴OB=$\sqrt{3}$OP=6$\sqrt{3}$,PB=2PO=12
∴B点坐标为(6$\sqrt{3}$,0),
∵Q是PB中点,P(0,6),B(6$\sqrt{3}$,0),
∴Q点坐标为(3$\sqrt{3}$,3)
∴OQ=$\frac{1}{2}$PB=6
∴以Q为圆心,OQ为半径的⊙Q的方程为(x-3$\sqrt{3}$)2+(y-3)2=36.
点评 此题是圆的综合题,主要考查了新定义,全等三角形的判定和性质,切线的判定,含30°的直角三角形的性质,解(1)的关键是判断出△POB≌△PAB,解(2)的关键是求出点B的坐标,是一道中等难度的题目.


科目:初中数学 来源:2016~2017学年安徽省芜湖市九年级下学期第一次模拟考试数学试卷(解析版) 题型:选择题
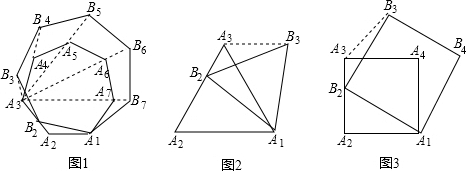
已知x=1是方程x +b x-2=0的一个根,则方程的另一个根是
+b x-2=0的一个根,则方程的另一个根是
A.1 B.2 C.-2 D.-1
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
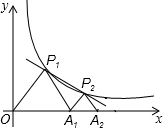 如图,P1、P2(P2在P1的右侧)是y=$\frac{k}{x}$(k>0)在第一象限上的两点,点A1的坐标为(2,0).
如图,P1、P2(P2在P1的右侧)是y=$\frac{k}{x}$(k>0)在第一象限上的两点,点A1的坐标为(2,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
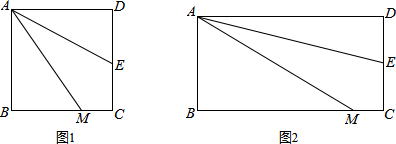
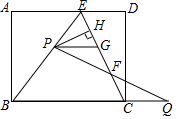 如图,在矩形ABCD中,E是AD上一点,AB=8,BE=BC=10,动点P在线段BE上(与点B、E不重合),点Q在BC的延长线上,PE=CQ,PQ交EC于点F,PG∥BQ交EC于点G,设PE=x.
如图,在矩形ABCD中,E是AD上一点,AB=8,BE=BC=10,动点P在线段BE上(与点B、E不重合),点Q在BC的延长线上,PE=CQ,PQ交EC于点F,PG∥BQ交EC于点G,设PE=x.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com