
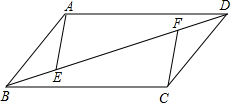
 如图所示,在平行四边形ABCD中,对角线AC,BD相交于点O,点E,F在对角线BD上,且 BE=DF.求证:
如图所示,在平行四边形ABCD中,对角线AC,BD相交于点O,点E,F在对角线BD上,且 BE=DF.求证:
|


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
| A、x(a-b)=ax-bx |
| B、x2-1+y2=(x-1)(x+1)+y2 |
| C、ax+bx+c=x(a+b)+c |
| D、x2-1=(x+1)(x-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,某班同学组织课外实践活动,预测量一建筑物DE的高度,在建筑物附近一斜坡A点测得建筑物顶端D的仰角为30°,在坡底C点测得建筑物顶端D烦人仰角为60°,已知A点烦人高度AB为20米,坡角∠ACB=45°,且B、C、E三点在同一条直线上,请根据以上条件求出建筑物DE的高度(测量器的高度忽略不计).
如图,某班同学组织课外实践活动,预测量一建筑物DE的高度,在建筑物附近一斜坡A点测得建筑物顶端D的仰角为30°,在坡底C点测得建筑物顶端D烦人仰角为60°,已知A点烦人高度AB为20米,坡角∠ACB=45°,且B、C、E三点在同一条直线上,请根据以上条件求出建筑物DE的高度(测量器的高度忽略不计).查看答案和解析>>
科目:初中数学 来源: 题型:
|
| a-2 |
| a+3 |
| a2-4 |
| 2a+6 |
| 5 |
| a+2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| ||
| 2 |
cosB-
|
| A、、105° | B、90° |
| C、、75° | D、、60° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com