

 ,
,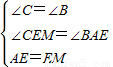 ,
, =
= ,
, =
=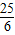 ,
, =
= .
.

科目:初中数学 来源: 题型:
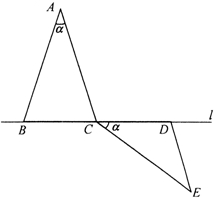 23、如图在△ABC和△CDE中,AB=AC=CE,BC=DC=DE,AB>BC,∠BAC=∠DCE=∠α,点B、C、D在直线l上,按下列要求画图(保留画图痕迹);
23、如图在△ABC和△CDE中,AB=AC=CE,BC=DC=DE,AB>BC,∠BAC=∠DCE=∠α,点B、C、D在直线l上,按下列要求画图(保留画图痕迹);查看答案和解析>>
科目:初中数学 来源: 题型:
 如图在△ABC和△DEF中,AB=AC=DE=DF=5,BC=EF=6,移动△DEF,在整个移动过程中,点E始终在BC边上(点E不经过B、C两点),且DE经过点A,设EF与AC的交点为M.
如图在△ABC和△DEF中,AB=AC=DE=DF=5,BC=EF=6,移动△DEF,在整个移动过程中,点E始终在BC边上(点E不经过B、C两点),且DE经过点A,设EF与AC的交点为M.查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏扬中市九年级下学期期中考试数学试卷(解析版) 题型:解答题
动手操作(本小题满分7分)
如图在△ABC和△CDE中,AB=AC=CE,BC=DC=DE,AB>BC,∠BAC=∠DCE=∠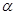 ,点B、C、D在直线l上,按下列要求画图(保留画图痕迹);
,点B、C、D在直线l上,按下列要求画图(保留画图痕迹);
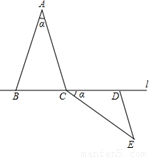
(1)画出点E关于直线l的对称点E’,连接CE’ 、DE’;
(2)以点C为旋转中心,将(1)中所得△CDE’ 按逆时针方向旋转,使得CE’与CA重合,
得到△CD’E’’(A).画出△CD’E’’(A).解决下面问题:
①线段AB和线段CD’的位置关系是 ▲ ;理由是: ▲ .
②求∠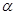 的度数.
的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com