
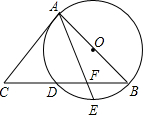
 如图,AB是⊙O的直径,AC是切⊙O于A的切线,BC交⊙O于点D,E是劣弧$\widehat{BD}$的中点,连接AE交BC于点F,若cosC=$\frac{2}{3}$,AC=6,则BF的长为3.
如图,AB是⊙O的直径,AC是切⊙O于A的切线,BC交⊙O于点D,E是劣弧$\widehat{BD}$的中点,连接AE交BC于点F,若cosC=$\frac{2}{3}$,AC=6,则BF的长为3. 分析 连接AD,由圆周角定理可得△ACD是直角三角形,作FH⊥AB于H,如图,利用余弦定义,在Rt△ACD中可计算出CD=4,在Rt△ACB中可计算出BC=9,则BD=BC-CD=5,接着根据角平分线性质得FD=FH,于是设BF=x,则DF=FH=5-x,然后利用平行线得性质由FH∥AC得到∠HFB=∠C,所以cos∠BFH=cosC的值可求出,再利用比例性质可求出BF.
解答 解:连接AD,作FH⊥AB于H,如图,
∵AB是⊙O的直径,
∴∠ADB=∠ADC=90°,
∴△ADC是直角三角形,
在Rt△ACD中,∵cosC=$\frac{CD}{AC}$=$\frac{2}{3}$,
∴CD=$\frac{2}{3}$×6=4,
∵AC是切⊙O于A的切线,
∴AC⊥AB,
∴△CAB是直角三角形
在Rt△ACB中,∵cosC=$\frac{AC}{BC}$=$\frac{2}{3}$,
∴BC=$\frac{3}{2}$×6=9,
∴BD=BC-CD=9-4=5,
∵∠EAB=∠EAD,即AF平分∠BAD,
而FD⊥AD,FH⊥AB,
∴FD=FH,
设BF=x,则DF=FH=5-x,
∵FH∥AC,
∴∠HFB=∠C,
在Rt△BFH中,∵cos∠BFH=cosC=$\frac{2}{3}$=$\frac{FH}{BF}$,
∴$\frac{5-x}{x}$=$\frac{2}{3}$,
解得x=3,
即BF的长为3.
故答案为:3.
点评 本题考查了切线的性质、圆周角定理的运用以及解直角三角形的有关知识点,题目的综合性较强,有一定的难度,正确做出图形的辅助线是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
 已知A,B两地公路长300km,甲、乙两车同时从A地出发沿同一公路驶往B地,2小时后,甲车接到电话需返回这条公路上与A地相距105km的C处取回货物,于是甲车立即原路返回C地,取了货物又立即赶往B地(取货物的时间忽略不计),结果两下车同时到达B地,两车的速度始终保持不变,设两车山发x小时后,甲、乙两车距离A地的路程分别为y1(km)和y2(km).它们的函数图象分别是折线OPQR和线段OR.
已知A,B两地公路长300km,甲、乙两车同时从A地出发沿同一公路驶往B地,2小时后,甲车接到电话需返回这条公路上与A地相距105km的C处取回货物,于是甲车立即原路返回C地,取了货物又立即赶往B地(取货物的时间忽略不计),结果两下车同时到达B地,两车的速度始终保持不变,设两车山发x小时后,甲、乙两车距离A地的路程分别为y1(km)和y2(km).它们的函数图象分别是折线OPQR和线段OR.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 四边形OBCD中的三个顶点在⊙O上,点A是⊙O上的一个动点(不与点B、C、D重合).若四边形OBCD是平行四边形时,那么∠OBA和∠ODA的数量关系是∠OBA-∠ODA=60°或∠OBA+∠ODA=60°或∠ODA-∠OBA=60°或∠OBA+∠ODA=120°.
四边形OBCD中的三个顶点在⊙O上,点A是⊙O上的一个动点(不与点B、C、D重合).若四边形OBCD是平行四边形时,那么∠OBA和∠ODA的数量关系是∠OBA-∠ODA=60°或∠OBA+∠ODA=60°或∠ODA-∠OBA=60°或∠OBA+∠ODA=120°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com