练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图，点P为□ABCD的边CD上一点，若△PAB、△PCD和△PBC的面积分别为
    s1、s2和s3，则它们之间的大小关系是(     )

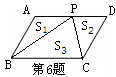
    A. S3=S1+S2         B. 2S3=S1+S2        C. S3>S1+S2        D. S3<S1+S2
    A
    分析：设平行四边形的高为h，然后分别表示出s1、s2和s3，即可得出三者的关系．
    解答：解：设平行四边形的高为h，
    则S1=×AP×h，S2=PD×h，S3=BC×h，
    又平心四边形的对边相等，
    ∴AP+PD=AD=BC，
    ∴S3=S1+S2．
    故选A．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：不详 题型：解答题

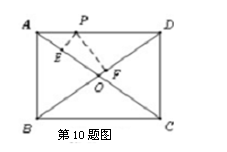
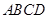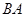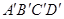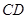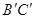    如图，把直角梯形沿方向平移得到梯形，与相交于点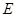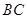，=20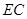cm，=5cm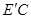，=4cm，图中阴影部分的面积与哪个四边形的面积相等，并求出阴影部分的面积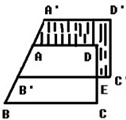

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：填空题

    菱形ABCD边长为4，点E在直线AD上，DE=3，联结BE与对角线AC交点M，那么的值是  ▲   .

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

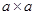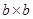    ）已知，如图，现有、的正方形纸片和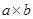的矩形纸片各若干块，试选用这些纸片（每种纸片至少用一次）在下面的虚线方框中拼成一个矩形（每两个纸片之间既不重叠，也无空隙，拼出的图中必须保留拼图的痕迹），使拼出的矩形面积为a2＋3ab＋2b2，并标出此矩形的长和宽．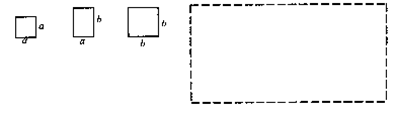

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    如图，在梯形ABCD中，AD∥BC，AB="DC" ，过点D作DE∥AB 交BC于点E．

    (1) 请你判断四边形ABED的形状，并说明理由；
    (2) 当△DEC为等边三角形时，
    ① 求∠B的度数；
    ② 若AD=4，DC=3，求等腰梯形ABCD的周长.

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：单选题

    如图，点P是矩形ABCD的边AD的一个动点，矩形的两条边AB、BC的长分别为3和4，那么点P到矩形的两条对角线AC和BD的距离之和是（    ）

    A．2.5　　      B．1.2　         C．2.4　　       D．4.8

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    如图，在平行四边形ABCD中，∠ABC、∠BCD的平分线相交于点O，BO延长线交CD延长线于点E，

    求证：OB=OE

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：单选题

    如图2，四边形ABCD的对角线AC、BD互相垂直，则下列条件能判定四边形ABCD为菱形的是（    ）

    A．BA＝BC      B．AC、BD互相平分       C．AC＝BD       D．AB∥CD

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：单选题

    不能判断四边形ABCD是平行四边形的是（　　）
    A．AB＝CD，AD＝BCB．AB＝CD，AB∥CD
    C．AB＝CD，AD∥BCD．AB∥CD，AD∥BC

    查看答案和解析>>

    同步练习册答案