
”¾ĢāÄæ”æŌŚ”÷ABCÖŠ£¬AB=6£¬AC=BC=5£¬½«”÷ABCČʵćA°“Ė³Ź±Õė·½ĻņŠż×Ŗ£¬µĆµ½”÷ADE£¬Šż×Ŗ½ĒĪŖ¦Į£Ø0”ć£¼¦Į£¼180”ć£©£¬µćBµÄ¶ŌÓ¦µćĪŖµćD£¬µćCµÄ¶ŌÓ¦µćĪŖµćE£¬Į¬½ÓBD£¬BE£®
£Ø1£©ČēĶ¼£¬µ±¦Į=60”揱£¬ŃÓ³¤BE½»ADÓŚµćF£®
¢ŁĒóÖ¤£ŗ”÷ABDŹĒµČ±ßČż½ĒŠĪ£»
¢ŚĒóÖ¤£ŗBF”ĶAD£¬AF=DF£»
¢ŪĒėÖ±½ÓŠ“³öBEµÄ³¤£»
£Ø2£©ŌŚŠż×Ŗ¹ż³ĢÖŠ£¬¹żµćD×÷DG“¹Ö±ÓŚÖ±ĻßAB£¬“¹×ćĪŖµćG£¬Į¬½ÓCE£¬µ±”ĻDAG=”ĻACB£¬ĒŅĻ߶ĪDGÓėĻ߶ĪAEĪŽ¹«¹²µćŹ±£¬ĒėÖ±½ÓŠ“³öBE+CEµÄÖµ£®
ĪĀÜ°ĢįŹ¾£ŗæ¼ÉśæÉŅŌøł¾ŻĢāŅā£¬ŌŚ±øÓĆĶ¼ÖŠ²¹³äĶ¼ŠĪ£¬ŅŌ±ć×÷“š£®
”¾“š°ø”æ
£Ø1£©
½ā£ŗ¢Ł”ß”÷ABCČʵćAĖ³Ź±Õė·½ĻņŠż×Ŗ60”ćµĆµ½”÷ADE£¬
”ąAB=AD£¬”ĻBAD=60”ć£¬
”ą”÷ABDŹĒµČ±ßČż½ĒŠĪ£»
¢ŚÓÉ¢ŁµĆ”÷ABDŹĒµČ±ßČż½ĒŠĪ£¬
”ąAB=BD£¬
”ß”÷ABCČʵćAĖ³Ź±Õė·½ĻņŠż×Ŗ60”ćµĆµ½”÷ADE£¬
”ąAC=AE£¬BC=DE£¬
ÓÖ”ßAC=BC£¬
”ąEA=ED£¬
”ąµćB”¢EŌŚADµÄÖŠ“¹ĻßÉĻ£¬
”ąBEŹĒADµÄÖŠ“¹Ļߣ¬
”ßµćFŌŚBEµÄŃÓ³¤ĻßÉĻ£¬
”ąBF”ĶAD£¬AF=DF£»
¢ŪÓÉ¢ŚÖŖBF”ĶAD£¬AF=DF£¬
”ąAF=DF=3£¬
”ßAE=AC=5£¬
”ąEF=4£¬
”ßŌŚµČ±ßČż½ĒŠĪABDÖŠ£¬BF=ABsin”ĻBAF=6”Į ![]() =3
=3 ![]() £¬
£¬
”ąBE=BF©EF=3 ![]() ©4
©4
£Ø2£©
½ā£ŗČēĶ¼ĖłŹ¾£¬

”ß”ĻDAG=”ĻACB£¬”ĻDAE=”ĻBAC£¬
”ą”ĻACB+”ĻBAC+”ĻABC=”ĻDAG+”ĻDAE+”ĻABC=180”ć£¬
Ó֔ߔĻDAG+”ĻDAE+”ĻBAE=180”ć£¬
”ą”ĻBAE=”ĻABC£¬
”ßAC=BC=AE£¬
”ą”ĻBAC=”ĻABC£¬
”ą”ĻBAE=”ĻBAC£¬
”ąAB”ĶCE£¬ĒŅCH=HE= ![]() CE£¬
CE£¬
”ßAC=BC£¬
”ąAH=BH= ![]() AB=3£¬
AB=3£¬
ŌņCE=2CH=8£¬BE=5£¬
”ąBE+CE=13£®
”¾½āĪö”æ£Ø1£©¢ŁÓÉŠż×ŖŠŌÖŹÖŖAB=AD£¬”ĻBAD=60”ć¼“æɵĆÖ¤£»¢ŚÓÉBA=BD”¢EA=EDøł¾ŻÖŠ“¹ĻߊŌÖŹ¼“æɵĆÖ¤£»¢Ū·Ö±šĒó³öBF”¢EFµÄ³¤¼“æÉµĆ£»£Ø2£©ÓÉ”ĻACB+”ĻBAC+”ĻABC=180”ć”¢”ĻDAG+”ĻDAE+”ĻBAE=180”ć”¢”ĻDAG=”ĻACB”¢”ĻDAE=”ĻBACµĆ”ĻBAE=”ĻBACĒŅAE=AC£¬øł¾ŻČżĻßŗĻŅ»æɵĆCE”ĶAB”¢AC=5”¢AH=3£¬¼Ģ¶ųÖŖCE=2CH=8”¢BE=5£¬¼“æɵƓš°ø£®±¾ĢāÖ÷ŅŖæ¼²éŠż×ŖµÄŠŌÖŹ”¢µČ±ßČż½ĒŠĪµÄÅŠ¶ØÓėŠŌÖŹ”¢ÖŠ“¹ĻߵĊŌÖŹ”¢Čż½ĒŠĪÄŚ½ĒŗĶ¶ØĄķµČÖŖŹ¶µć£¬ŹģĮ·ÕĘĪÕŠż×ŖµÄŠŌÖŹŹĒ½āĢāµÄ¹Ų¼ü£®
”¾æ¼µć¾«Īö”æ½ā“š“ĖĢāµÄ¹Ų¼üŌŚÓŚĄķ½āČż½ĒŠĪµÄÄŚ½ĒŗĶĶā½ĒµÄĻą¹ŲÖŖŹ¶£¬ÕĘĪÕČż½ĒŠĪµÄČżøöÄŚ½ĒÖŠ£¬Ö»æÉÄÜÓŠŅ»øöÄŚ½ĒŹĒÖ±½Ē»ņ¶Ū½Ē£»Ö±½ĒČż½ĒŠĪµÄĮ½øöČń½Ē»„Óą£»Čż½ĒŠĪµÄŅ»øöĶā½ĒµČÓŚŗĶĖü²»ĻąĮŚµÄĮ½øöÄŚ½ĒµÄŗĶ£»Čż½ĒŠĪµÄŅ»øöĶā½Ē“óÓŚČĪŗĪŅ»øöŗĶĖü²»ĻąĮŚµÄÄŚ½Ē£¬ŅŌ¼°¶ŌŠż×ŖµÄŠŌÖŹµÄĄķ½ā£¬ĮĖ½ā¢ŁŠż×Ŗŗó¶ŌÓ¦µÄĻ߶Ī³¤¶Ģ²»±ä£¬Šż×Ŗ½Ē¶Č“󊔲»±ä£»¢ŚŠż×Ŗŗó¶ŌÓ¦µÄµćµ½Šż×Ŗµ½Šż×ŖÖŠŠÄµÄ¾ąĄė²»±ä£»¢ŪŠż×ŖŗóĪļĢå»ņĶ¼ŠĪ²»±ä£¬Ö»ŹĒĪ»ÖƱäĮĖ£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬”ĻBAC=45”ć£¬AB=4cm£¬½«”÷ABCČʵćB°“ÄꏱÕė·½ĻņŠż×Ŗ45”ćŗóµĆµ½”÷A”äBC”䣬ŌņŅõÓ°²æ·ÖµÄĆ껿ĪŖcm2 £® 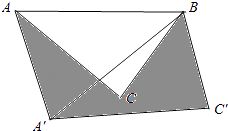
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijÉĢ³”ĻśŹŪ¹śĶā”¢¹śÄŚĮ½ÖÖĘ·ÅʵÄÖĒÄÜŹÖ»ś£¬ÕāĮ½ÖÖŹÖ»śµÄ½ų¼ŪŗĶŹŪ¼ŪČē±ķĖłŹ¾
¹śĶāĘ·ÅĘ | ¹śÄŚĘ·ÅĘ | |
½ų¼Ū£ØĶņŌŖ/²æ£© | 0.44 | 0.2 |
ŹŪ¼Ū£ØĶņŌŖ/²æ£© | 0.5 | 0.25 |
øĆÉĢ³”¼Ę»®¹ŗ½ųĮ½ÖÖŹÖ»śČōøɲ棬¹²Šč14.8ĶņŌŖ£¬Ō¤¼ĘČ«²æĻśŹŪŗóæÉ»ńĆ«ĄūČó¹²2.7ĶņŌŖ£®[Ć«ĄūČó=£ØŹŪ¼Ū©½ų¼Ū£©”ĮĻśŹŪĮæ]
£Ø1£©øĆÉĢ³”¼Ę»®¹ŗ½ų¹śĶāĘ·ÅĘ”¢¹śÄŚĘ·ÅĘĮ½ÖÖŹÖ»śø÷¶ąÉŁ²æ£æ
£Ø2£©ĶعżŹŠ³”µ÷ŃŠ£¬øĆÉĢ³”¾ö¶ØŌŚŌ¼Ę»®µÄ»ł“”ÉĻ£¬¼õÉŁ¹śĶāĘ·ÅĘŹÖ»śµÄ¹ŗ½ųŹżĮ棬Ōö¼Ó¹śÄŚĘ·ÅĘŹÖ»śµÄ¹ŗ½ųŹżĮ森ŅŃÖŖ¹śÄŚĘ·ÅĘŹÖ»śŌö¼ÓµÄŹżĮæŹĒ¹śĶāĘ·ÅĘŹÖ»ś¼õÉŁµÄŹżĮæµÄ3±¶£¬¶ųĒŅÓĆÓŚ¹ŗ½ųÕāĮ½ÖÖŹÖ»śµÄ×Ü׏½š²»³¬¹ż15.6ĶņŌŖ£¬øĆÉĢ³”Ó¦øĆŌõŃł½ų»õ£¬Ź¹Č«²æĻśŹŪŗó»ńµĆµÄĆ«ĄūČó×ī“ó£æ²¢Ēó³ö×ī“óĆ«ĄūČó
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬”÷ABC”Õ”÷ABD£¬µćEŌŚ±ßABÉĻ£¬CE”ĪBD£¬Į¬½ÓDE£®ĒóÖ¤£ŗ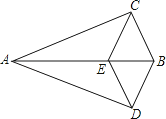
£Ø1£©”ĻCEB=”ĻCBE£»
£Ø2£©ĖıߊĪBCEDŹĒĮāŠĪ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬ŅŌABĪŖÖ±¾¶µÄ”ŃO·Ö±šÓŚBC£¬ACĻą½»ÓŚµćD£¬E£¬BD=CD£¬¹żµćD×÷”ŃOµÄĒŠĻß½»±ßACÓŚµćF£®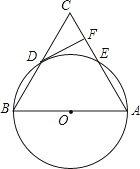
£Ø1£©ĒóÖ¤£ŗDF”ĶAC£»
£Ø2£©Čō”ŃOµÄ°ė¾¶ĪŖ5£¬”ĻCDF=30”ć£¬Ēó ![]() µÄ³¤£Ø½į¹ū±£Įō¦Š£©£®
µÄ³¤£Ø½į¹ū±£Įō¦Š£©£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŖĻģÓ¦”°ŹéĻćŠ£ĻģŌ°”±½ØÉčµÄŗÅÕŁ£¬ŌŚČ«Š£ŠĪ³ÉĮ¼ŗƵÄŌĶĮ·ÕĪ§£¬Ė껜µ÷²éĮĖ²æ·ÖŃ§ÉśĘ½¾łĆæĢģŌĶĮŹ±¼ä£¬Ķ³¼Ę½į¹ūČēĶ¼ĖłŹ¾£¬Ōņ±¾“Īµ÷²éÖŠŌĶĮŹ±¼äĪŖµÄÖŚŹżŗĶÖŠĪ»Źż·Ö±šŹĒ£Ø £© 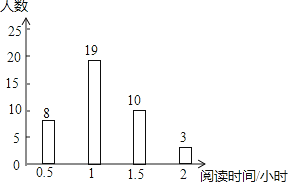
A.2ŗĶ1
B.1.25ŗĶ1
C.1ŗĶ1
D.1ŗĶ1.25
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
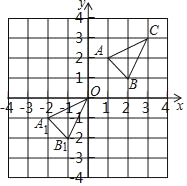
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖ”÷ABC¾¹żĘ½ŅĘŗóµĆµ½”÷A1B1C1£¬µćAÓėA1£¬µćBÓėB1£¬µćCÓėC1·Ö±šŹĒ¶ŌÓ¦µć£¬¹Ū²ģø÷¶ŌÓ¦µć×ų±źÖ®¼äµÄ¹ŲĻµ£¬½ā“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©·Ö±šŠ“³öµćAÓėA1£¬µćBÓėB1£¬µćCÓėC1µÄ×ų±ź£»
£Ø2£©ČōµćP£Øx£¬y£©ĶعżÉĻŹöµÄĘ½ŅĘ¹ęĀÉĘ½ŅʵƵ½µÄ¶ŌÓ¦µćĪŖQ£Ø3£¬5£©£¬Ēópµć×ų±ź£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ׊ĻøŌĶĮĻĀĆ꥿Ģā£¬½ā“šĪŹĢā
ĄżĢā£ŗŅŃÖŖ¶ž“ĪČżĻīŹ½x2©4x+mÓŠŅ»øöŅņŹ½ŹĒ£Øx+3£©£¬ĒóĮķŅ»øöŅņŹ½ŅŌ¼°mµÄÖµ£®
½ā£ŗÉčĮķŅ»øöŅņŹ½ĪŖ£Øx+n£©£¬µĆx2©4x+m£½£Øx+3£©£Øx+n£©£¬
Ōņx2©4x+m£½x2+£Øn+3£©x+3n
”ą![]()
½āµĆ£ŗn£½©7£¬m£½©21£®
”ąĮķŅ»øöŅņŹ½ĪŖ£Øx©7£©£¬mµÄÖµĪŖ©21£®
ĪŹĢā£ŗ
£Ø1£©Čō¶ž“ĪČżĻīŹ½x2©5x+6æÉ·Ö½āĪŖ£Øx©2£©£Øx+a£©£¬Ōņa£½”” ””£»
£Ø2£©Čō¶ž“ĪČżĻīŹ½2x2+bx©5æÉ·Ö½āĪŖ£Ø2x©1£©£Øx+5£©£¬Ōņb£½”” ””£»
£Ø3£©·ĀÕÕŅŌÉĻ·½·Ø½ā“šĻĀĆęĪŹĢā£ŗČō¶ž“ĪČżĻīŹ½2x2+3x©kÓŠŅ»øöŅņŹ½ŹĒ£Ø2x©5£©£¬ĒóĮķŅ»øöŅņŹ½ŅŌ¼°kµÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”收¾ÅÕĀĖćŹõ”·ŹĒĪŅ¹ś¹Å“śÄŚČŻ¼«ĪŖ·įø»µÄŹżŃ§ĆūÖų”£ŹéÖŠÓŠĻĀĮŠĪŹĢā”°½ńÓŠ¹“°Ė²½£¬¹ÉŹ®Īå²½”£ĪŹ¹“ÖŠČŻŌ²¾¶¼øŗĪ£æ”±ĘäŅāĖ¼ĪŖ½ńÓŠÖ±½ĒČż½ĒŠĪ£¬¹“£Ø¶ĢÖ±½Ē±ß£©³¤ĪŖ8²½£¬¹É£Ø³¤Ö±½Ē±ß£©³¤ĪŖ15²½£¬ĪŹøĆÖ±½ĒČż½ĒŠĪÄÜČŻÄɵÄŌ²ŠĪ£ØÄŚĒŠŌ²£©Ö±¾¶ŹĒ²½”£
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com