
【题目】如图,在四边形![]() 中,
中,![]() ∥
∥![]() ,
,![]() =2
=2![]() ,
,![]() 为
为![]() 的中点,请仅用无刻度的直尺分别按下列要求画图(保留作图痕迹)
的中点,请仅用无刻度的直尺分别按下列要求画图(保留作图痕迹)
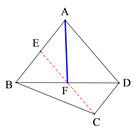
(1)在图1中,画出△ABD的BD边上的中线;
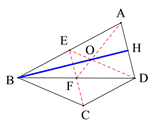
(2)在图2中,若BA=BD, 画出△ABD的AD边上的高 .

【答案】(1)作图见解析;(2)作图见解析.
【解析】(1)根据AB=2CD,AB=BE,可知BE=CD,再根据BE//CD,可知连接CE,CE与BD的交点F即为BD的中点,连接AF,则AF即为△ABD的BD边上的中线;
(2)由(1)可知连接CE与BD交于点F,则F为BD的中点,根据三角形中位线定理可得EF//AD,EF=![]() AD,则可得四边形ADFE要等腰梯形,连接AF,DE交于点O,根据等腰梯形的性质可推导得出OA=OD,再结合BA=BD可知直线BO是线段AD的垂直平分线,据此即可作出可得△ABD的AD边上的高 .
AD,则可得四边形ADFE要等腰梯形,连接AF,DE交于点O,根据等腰梯形的性质可推导得出OA=OD,再结合BA=BD可知直线BO是线段AD的垂直平分线,据此即可作出可得△ABD的AD边上的高 .
(1)如图AF是△ABD的BD边上的中线;
(2)如图AH是△ABD的AD边上的高.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
【题目】在□ABCD中,E为BC的中点,过点E作EF⊥AB于点F,延长DC,交FE的延长线于点G,连结DF,已知∠FDG=45°
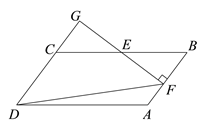
(1)求证:GD=GF.
(2)已知BC=10, ![]() .求 CD的长.
.求 CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为2cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积为1cm2,则它移动的距离AA′等于( )

A. 0.5cm B. 1cm C. 1.5cm D. 2cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂为了检验甲、乙两车间生产的同一款新产品的合格情况(尺寸范围为![]() ~
~![]() 的产品为合格〉.随机各抽取了20个祥品迸行检测.过程如下:
的产品为合格〉.随机各抽取了20个祥品迸行检测.过程如下:
收集数据(单位:![]() ):
):
甲车间:168,175,180,185,172,189,185,182,185,174,192,180,185,178,173,185,169,187,176,180.
乙车间:186,180,189,183,176,173,178,167,180,175,178,182,180,179,185,180,184,182,180,183.
整理数据:
组别频数 | 165.5~170.5 | 170.5~175.5 | 175.5~180.5 | 180.5~185.5 | 185.5~190.5 | 190.5~195.5 |
甲车间 | 2 | 4 | 5 | 6 | 2 | 1 |
乙车间 | 1 | 2 |
|
| 2 | 0 |
分析数据:
车间 | 平均数 | 众数 | 中位数 | 方差 |
甲车间 | 180 | 185 | 180 | 43.1 |
乙车间 | 180 | 180 | 180 | 22.6 |
应用数据;
(1)计算甲车间样品的合格率.
(2)估计乙车间生产的1000个该款新产品中合格产品有多少个?
(3)结合上述数据信息.请判断哪个车间生产的新产品更好.并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB是⊙O的直径,AD与⊙O相切于点A,DE与⊙O相切于点E,点C为DE延长线上一点,且CE=CB.
(1)求证:BC为⊙O的切线;
(2)若AB=4,AD=1,求线段CE的长.
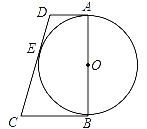
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() 分别是
分别是![]() 的中点,若等腰
的中点,若等腰![]() 绕点
绕点![]() 逆时针旋转,得到等腰
逆时针旋转,得到等腰![]() ,设旋转角为
,设旋转角为![]() ,记直线
,记直线![]() 与
与![]() 的交点为
的交点为![]()


(1)如图![]() ,当
,当![]() 时,线段
时,线段![]() 的长等于 ,线段
的长等于 ,线段![]() 的长等于 .(直接填写结果)
的长等于 .(直接填写结果)
(2)如图![]() ,当
,当![]() 时,求证:
时,求证:![]() ,且
,且![]() ;
;
(3)设![]() 的中点为
的中点为![]() ,则线段
,则线段![]() 的长为 (直接填写结果).
的长为 (直接填写结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥EF,则∠A、∠C、∠D、∠E满足的数量关系是( )
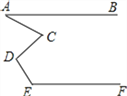
A. ∠A+∠C+∠D+∠E=360°
B. ∠A+∠D=∠C+∠E
C. ∠A-∠C+∠D+∠E=180°
D. ∠E-∠C+∠D-∠A=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
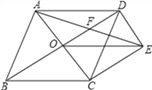
【题目】如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=![]() AC,连接AE交OD于点F,连接CE、OE.
AC,连接AE交OD于点F,连接CE、OE.
(1)求证:OE=CD;
(2)若菱形ABCD的边长为2,∠ABC=60°,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了增强学生体质,决定开设以下体育课外活动项目:A.篮球 B.乒乓球C.羽毛球 D.足球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,

请回答下列问题:
(1)这次被调查的学生共有多少人?
(2)请你将条形统计图(2)补充完整;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com