
【题目】四个数分别是![]() ,满足
,满足![]() ,(且
,(且![]() 为正整数,
为正整数,![]() ).
).
![]() 若
若![]() .
.
①当![]() 时,求
时,求![]() 的值;
的值;
②对于给定的有理数![]() ,满足
,满足![]() ,请用含
,请用含![]() 的代数式表示
的代数式表示![]() ;
;
![]() 若
若 ![]() ,
,![]() ,且
,且![]() ,试求
,试求![]() 的最大值.
的最大值.
【答案】(1)①![]() ;②
;②![]() ;(2)
;(2)![]() 的最大值为
的最大值为![]() .
.
【解析】
方法一:
![]() ①根据
①根据![]() 和绝对值的性质去掉绝对值符号,再利用它们之间的关系即可得出答案;
和绝对值的性质去掉绝对值符号,再利用它们之间的关系即可得出答案;
②同样先去掉绝对值符号,通过等量代换和第(1)问中的结论得出![]() ,则答案可得;
,则答案可得;
![]() 同样先将e,f去掉绝对值符号,然后表示出
同样先将e,f去掉绝对值符号,然后表示出![]() ,然后利用
,然后利用![]() 建立一个关于n的不等式,解不等式即可找到答案.
建立一个关于n的不等式,解不等式即可找到答案.
方法二:
![]() ①将四个数表示在数轴上,然后转化已知条件为
①将四个数表示在数轴上,然后转化已知条件为![]() ,然后利用两点间的距离即可得出答案;
,然后利用两点间的距离即可得出答案;
②用点![]() 表示数
表示数![]() 在数轴上表述出来,得出
在数轴上表述出来,得出![]() 进而得出
进而得出![]() 则答案可得;
则答案可得;
![]() 直接将e,f代入得出
直接将e,f代入得出![]() ,再利用
,再利用![]() 得出
得出![]() ,则答案可得.
,则答案可得.
方法一:
![]() ①
①![]() ,
,
![]() ,
,
![]()
![]()
![]() ,
,
![]() ,
,
![]() .
.
②![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,即
,即![]()
![]() ,
,
![]() ,
,
![]() ,且
,且![]() 为正整数,
为正整数,
![]() 的最大值为
的最大值为![]() .
.
方法二:
![]() ①把
①把![]() 四个数在数轴上分别用点
四个数在数轴上分别用点![]() 表示出来,如下图所示,
表示出来,如下图所示,

![]() ,
,
![]()
又![]()
![]()
![]() .
.
②![]() 用点
用点![]() 表示数
表示数![]() 在数轴上表述出来,点
在数轴上表述出来,点![]() 在线段
在线段![]() 上,
上,

![]()
![]()
又![]() ,
,
![]()
即![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]() ,且
,且![]()
![]()
![]() ,即
,即![]()
![]()
![]()
![]()
![]() ,且
,且![]() 为正整数,
为正整数,
![]() 的最大值为
的最大值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某校七年级全体学生在5名教师的带领下去公园秋游,公园的门票为每人30元.现有两种优惠方案,甲方案:带队老师免费,学生按8折收费;乙方案:师生都按7.5折收费.
(1)若有n名学生,用含n的代数式表示两种优惠方案各需多少元?
(2)当n=70时,采用哪种方案更优惠?
(3)当n=100时,采用哪种方案更优惠?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各题(直接写出答案)
(1)2+(﹣2)= ;
(2)1﹣3= ;
(3)(﹣1)×(﹣3)= ;
(4)12÷(﹣3)= ;
(5)﹣32×![]() = ;
= ;
(6)(﹣4)2018×(﹣0.25)2019= ;
查看答案和解析>>
科目:初中数学 来源: 题型:
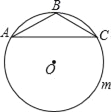
【题目】如图,△ABC中,AB=BC,∠ABC=120°,AC=2![]() ,⊙O是△ABC的外接圆,D是优弧AmC上任意一点(不包括A,C),记四边形ABCD的周长为y,BD的长为x,则y关于x的函数关系式是( )
,⊙O是△ABC的外接圆,D是优弧AmC上任意一点(不包括A,C),记四边形ABCD的周长为y,BD的长为x,则y关于x的函数关系式是( )
A. y=![]() x+4 B. y=
x+4 B. y=![]() x+4 C. y=
x+4 C. y=![]() x2+4 D. y=
x2+4 D. y=![]() x2+4
x2+4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD、DEFG都是正方形,连接AE、CG.

(1)求证:AE=CG;
(2)观察图形,猜想AE与CG之间的位置关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
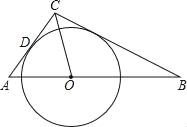
【题目】如图,在△ABC中,∠C=90°,∠ACB的平分线交AB于点O,以O为圆心的⊙O与AC相切于点D.
(1)求证:⊙O与BC相切;
(2)当AC=3,BC=6时,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义一种运算:![]() ,其中k是正整数,且k ≥2,[x]表示非负实数x的整数部分,例如[2.6]=2,[0.8]=0.若
,其中k是正整数,且k ≥2,[x]表示非负实数x的整数部分,例如[2.6]=2,[0.8]=0.若![]() ,则
,则![]() 的值为( )
的值为( )
A.2015B.4C.2014D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小炎遇到这样一个问题:如图1,点E、F分别在正方形ABCD的边BC,CD上,∠EAF=45°,连结EF,则EF=BE+DF,试说明理由.

小炎是这样思考的:要想解决这个问题,首先应想办法将这些分散的线段相对集中.她先后尝试了翻折、旋转、平移的方法,最后发现线段AB,AD是共点并且相等的,于是找到解决问题的方法.她的方法是将△ABE绕着点A逆时针旋转90°得到△ADG,再利用全等的知识解决了这个问题(如图2).
参考小炎同学思考问题的方法,解决下列问题:
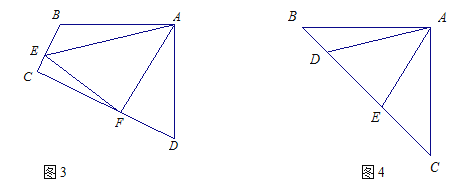
(1)如图3,四边形ABCD中,AB=AD,∠BAD=90°点E,F分别在边BC,CD上,∠EAF=45°.若∠B,∠D都不是直角,则当∠B与∠D满足_ 关系时,仍有EF=BE+DF;
(2)如图4,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°,若BD=1, EC=2,求DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com