
【题目】如图,在![]() 中,
中,![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,![]() ,延长
,延长![]() 到点F,使得
到点F,使得![]() ,连结
,连结![]() .
.

(1)求证:四边形![]() 是菱形;
是菱形;
(2)若![]() ,
,![]() ,求菱形
,求菱形![]() 的面积.
的面积.
【答案】(1)见解析;(2)![]()
【解析】
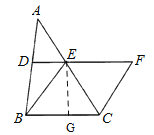
(1)从所给的条件可知,DE是△ABC的中位线,所以DE∥BC且2DE=BC,所以BC和EF平行且相等,所以四边形BCFE是平行四边形,又因为BE=EF,所以是菱形;
(2)由∠BEF是120°,可得∠EBC为60°,即可得△BEC是等边三角形,求得BE=BC=CE=5,再过点E作EG⊥BC于点G,求出高EG的长,即可求得答案.
解:(1)∵D、E分别是AB、AC的中点,
∴DE∥BC且2DE=BC,
又∵BE=2DE,EF=BE,
∴EF=BC,EF∥BC,
∴四边形BCFE是平行四边形,
又∵BE=EF,
∴四边形BCFE是菱形;
(2)∵∠BEF=120°,
∴∠EBC=60°,
∴△EBC是等边三角形,
∴BE=BC=CE=5,
过点E作EG⊥BC于点G,
∴EG=BEsin60°=5×![]() ,
,
∴S菱形BCFE=BCEG=5×![]() .
.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】△ABC的顶点均在边长为1的小正方形网络中的格点上,如图,建立平面直角坐标系,点B在x轴上.
(1)在图中画出△ABC关于x轴对称的△A’B’C’,连接AA’,求证:△AA’C≌△A’AC’;
(2)请在y轴上画点P,使得PB+PC最短.(保留作图痕迹,不写画法)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】你能求(x﹣1)(x99+x98+x97+…+x+1)的值吗?
遇到这样的问题,我们可以先思考一下,从简单的情形入手.先计算下列各式的值:
(1)(x﹣1)(x+1)= ;
(2)(x﹣1)(x2+x+1)= ;
(3)(x﹣1)(x3+x2+x+1)= ;
由此我们可以得到(x﹣1)(x99+x98+…+x+1)= ;
请你利用上面的结论,完成下面两题的计算:
(1)299+298+…+2+1;
(2)(﹣3)50+(﹣3)49+…+(﹣3)+1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学新建了一栋7层的教学大楼,每层楼有8间教室,进出这栋大楼共有八道门,其中四道正门大小相同,四道侧门大小也相同.安全检查中,对八道门进行了测试:当同时开启一道正门和两道侧门时,2分内可以通过560名学生;当同时开启一道正门和一道侧门时,4分内可以通过800名学生.
(1)平均每分内一道正门和一道侧门分别可以通过多少名学生?
(2)检查中发现,紧急情况时因学生拥挤,出门的效率将降低30%.安全检查规定:在紧急情况下全大楼的学生应在5分内通过这八道门安全撤离,假设这栋教学大楼每间教室最多有45名学生,问建造的这八道门是否符合安全规定?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为美化校园,计划对某一区域进行绿化,安排甲.乙 两个工程队完成;已知甲队每天能完成绿化面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为400![]() 区域的绿化时,甲队比乙队少用4天,求甲.乙两工程队每天能完成绿化的面积分别是多少
区域的绿化时,甲队比乙队少用4天,求甲.乙两工程队每天能完成绿化的面积分别是多少![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面的统计图表示某体校射击队甲、乙两名队员射击比赛的成绩,根据统计图中的信息,下列结论正确的是( )

A. 甲队员成绩的平均数比乙队员的大
B. 乙队员成绩的平均数比甲队员的大
C. 甲队员成绩的中位数比乙队员的大
D. 甲队员成绩的方差比乙队员的大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C在⊙O上,∠ABC=29°,过点C作⊙O的切线交OA的延长线于点D,则∠D的大小为( )
A.29°
B.32°
C.42°
D.58°
查看答案和解析>>
科目:初中数学 来源: 题型:
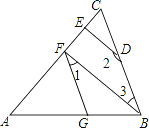
【题目】如图,∠AGF=∠ABC,∠1+∠2=180°.
(1)试判断BF与DE的位置关系,并说明理由;
(2)若BF⊥AC,∠2=150°,求∠AFG的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com