
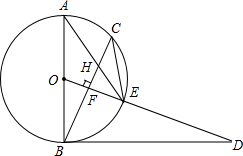
 已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.
已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.分析 (1)由圆周角定理和已知条件证出∠ODB=∠ABC,再证出∠ABC+∠DBF=90°,即∠OBD=90°,即可得出BD是⊙O的切线;
(2)连接AC,由垂径定理得出$\widehat{BE}=\widehat{CE}$,得出∠CAE=∠ECB,再由公共角∠CEA=∠HEC,证明△CEH∽△AEC,得出对应边成比例$\frac{CE}{EH}=\frac{EA}{CE}$,即可得出结论;
(3)连接BE,由圆周角定理得出∠AEB=90°,由三角函数求出BE,再根据勾股定理求出EA,得出BE=CE=6,由(2)的结论求出EH,然后根据勾股定理求出BH即可.
解答 (1)证明:∵∠ODB=∠AEC,∠AEC=∠ABC,
∴∠ODB=∠ABC,
∵OF⊥BC,
∴∠BFD=90°,
∴∠ODB+∠DBF=90°,
∴∠ABC+∠DBF=90°,
即∠OBD=90°,
∴BD⊥OB,
∴BD是⊙O的切线;
(2)证明:连接AC,如图1所示:
∵OF⊥BC,
∴$\widehat{BE}=\widehat{CE}$,
∴∠CAE=∠ECB,
∵∠CEA=∠HEC,
∴△CEH∽△AEC,
∴$\frac{CE}{EH}=\frac{EA}{CE}$,
∴CE2=EH•EA;
(3)解:连接BE,如图2所示:
∵AB是⊙O的直径,
∴∠AEB=90°,
∵⊙O的半径为5,sin∠BAE=$\frac{3}{5}$,
∴AB=10,BE=AB•sin∠BAE=10×$\frac{3}{5}$=6,
∴EA=$\sqrt{A{B}^{2}-B{E}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
∵$\widehat{BE}=\widehat{CE}$,
∴BE=CE=6,
∵CE2=EH•EA,
∴EH=$\frac{{6}^{2}}{8}$=$\frac{9}{2}$,
在Rt△BEH中,BH=$\sqrt{B{E}^{2}+E{H}^{2}}$=$\sqrt{{6}^{2}+(\frac{9}{2})^{2}}$=$\frac{15}{2}$.
点评 本题是圆的综合题目,考查了切线的判定、圆周角定理、圆心角、弧、弦之间的关系定理、勾股定理、三角函数、相似三角形的判定与性质等知识;本题难度较大,综合性强,特别是(2)(3)中,需要通过作辅助线证明三角形相似和运用三角函数、勾股定理才能得出结果.


科目:初中数学 来源: 题型:解答题
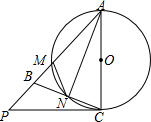 已知:如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点M,交BC于点N,连接AN,过点C的切线交AB的延长线于点P.
已知:如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点M,交BC于点N,连接AN,过点C的切线交AB的延长线于点P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
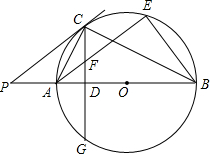 如图,AB为⊙O的直径,P是BA延长线上一点,PC切⊙O于点C,CG是⊙O的弦,CG⊥AB,垂足为D.
如图,AB为⊙O的直径,P是BA延长线上一点,PC切⊙O于点C,CG是⊙O的弦,CG⊥AB,垂足为D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
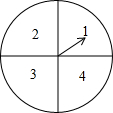 某超市计划在“十周年”庆典当天开展购物抽奖活动,凡当天在该超市购物的顾客,均有一次抽奖的机会,抽奖规则如下:将如图所示的圆形转盘平均分成四个扇形,分别标上1,2,3,4四个数字,抽奖者连续转动转盘两次,当每次转盘停止后指针所指扇形内的数为每次所得的数(若指针指在分界线时重转);当两次所得数字之和为8时,返现金20元;当两次所得数字之和为7时,返现金15元;当两次所得数字之和为6时返现金10元.
某超市计划在“十周年”庆典当天开展购物抽奖活动,凡当天在该超市购物的顾客,均有一次抽奖的机会,抽奖规则如下:将如图所示的圆形转盘平均分成四个扇形,分别标上1,2,3,4四个数字,抽奖者连续转动转盘两次,当每次转盘停止后指针所指扇形内的数为每次所得的数(若指针指在分界线时重转);当两次所得数字之和为8时,返现金20元;当两次所得数字之和为7时,返现金15元;当两次所得数字之和为6时返现金10元.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{4}$=±2 | B. | x2•x3=x6 | C. | $\sqrt{3}$+$\sqrt{2}$=$\sqrt{5}$ | D. | (x2)3=x6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com