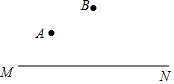练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    5．A、B两厂在公路MN同侧，拟在公路边建一货场C，若由B厂独家兴建，并考虑B厂的利益，则要求货场离B厂最近，请在图中作出此时货场C的位置，并说出这样做的道理．

    分析 通过点B作公路所在直线的垂线段BD，垂足C就是所求的点．

    解答 解：
    如图所示：

    理由：过直线外一点，向直线所作的线段中，垂线段最短．

    点评 本题考查了尺规作图，正确理解垂线的性质是作图的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

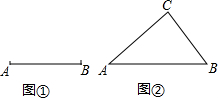    15．定义：如果三角形有一边上的中线长恰好等于这边的长，那么称这个三角形为“奇异三角形”，这条中线为“奇异中线”．
    （1）请根据定义解答：
    ①判断，命题：“如果直角三角形是奇异三角形，那么奇异中线一定是较长直角边上的中线”是真命题还是假命题；
    ②请用直尺和圆规在图①中画一个以AB为边的“奇异三角形”；
    （2）如图②，在Rt△ABC中，∠C=90°，$\frac{BC}{AC}$=$\frac{\sqrt{3}}{2}$，求证：△ABC是“奇异三角形”．
    （3）已知，等腰△ABC是“奇异三角形”，AB=AC=20，求底边BC的长．（结果保留根号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．平面直角坐标系内的一条直线同时满足下列两个条件：①不经过第四象限；②与两条坐标轴所围成的三角形的面积为2，这条直线的解析式可以是y=x+2（写出一个解析式即可）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

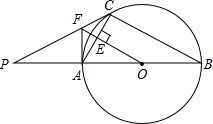    13．如图，C是以AB为直径的⊙O上一点，过O作OE⊥AC于点E，过点A作⊙O的切线交OE的延长线于点F，连接CF并延长交BA的延长线于点P．
    （1）求证：PC是⊙O的切线．
    （2）若AF=1，OA=2$\sqrt{2}$，求PC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．已知a＜0，则化简$\sqrt{-{a}^{3}b}$的结果是-a$\sqrt{-ab}$，．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．化简：
    （1）$\frac{4}{{x}^{2}-4}$+$\frac{2}{x+2}$-$\frac{1}{x-2}$；
    （2）$\frac{x-4}{4{x}^{2}-9}$÷$\frac{1}{2x+3}$+$\frac{x+1}{2x-3}$；
    （3）1-$\frac{a-1}{a}$÷（$\frac{a}{a+2}$-$\frac{1}{{a}^{2}+2a}$）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．化简：$\frac{x+1}{x-1}$-$\frac{4x}{{x}^{2}-1}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．如图，四边形ABCD中，∠ABC=∠ADC=90°，E、F分别是AC、BD的中点，∠BAC=15°，∠DAC=45°，则$\frac{EF}{CD}$的值为$\frac{\sqrt{2}}{4}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

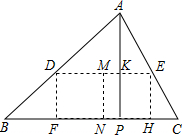    5．如图，△ABC是一块锐角三角形余料，边长BC=120cm，高AP=90cm，现在要把它加工成长方形零件DFHE，且满足FH=2DF，F、H在BC上，D、E分别在AB、AC上，求短边DF的长．

    查看答案和解析>>

    同步练习册答案