研究下列算式，你会发现有什么规律？
①13=12
②13+23=32
③13+23+33=62
④13+23+33+43=102
⑤13+23+33+43+53=152…
（1）根据以上算式的规律，请你写出第⑥个算式；
（2）用含n（n为正整数）的式子表示第n个算式；
（3）请用上述规律计算：73+83+93+…+203．
解：（1）第⑥个算式为1
3+2
3+3
3+4
3+5
3+6
3=21
2；
（2）第n个算式为
；
（3）7
3+8
3+9
3+…+20
3=（1
3+2
3+3
3+4
3+…+20
3）-（1
3+2
3+3
3+4
3+5
3+6
3）
=
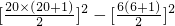
=44100-441=43659．
分析：（1）利用类比的方法得到第⑥个算式为 1
3+2
3+3
3+4
3+5
3+6
3=21
2；
（2）同样利用类比的方法得到第n个算式为
；
（3）将7
3+8
3+9
3+…+20
3转化为（1
3+2
3+3
3+4
3+…+20
3）-（1
3+2
3+3
3+4
3+5
3+6
3）后代入总结的规律求解即可．
点评：本题考查了数字的变化类问题，仔细观察每个算式得到本题的通项公式是解决此题的关键．
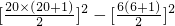
冲刺100分1号卷系列答案
=（2x+
．