
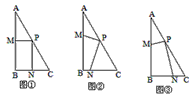
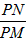 的值;
的值;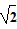 PA,点M、N分别在线段AB、BC上(如图③)时,求
PA,点M、N分别在线段AB、BC上(如图③)时,求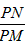 的值。
的值。解:(1) ; ; |
|
| (2)过点P作PE⊥AB于点E,PF⊥BC于点F, 则∠PEM=∠PFN=90°, 又∠ABC=90°, ∴四边形BFPE是矩形, ∴∠EPF=90°, ∵∠MPN=90°, ∴∠MPE+∠EPN=∠NPF+∠EPN=90° ∴∠MPE=∠NPF, ∴△PFN∽△PEM, ∴  ,由(1)可知PF= ,由(1)可知PF= PE,∴ PE,∴ = = ; ; |
 |
| (3)在Rt△ABC中,过点P作PE⊥AB于E,PF⊥BC于点F, ∴四边形BFPE是矩形, ∴∠EPF=90°, ∵∠EPM+∠MPF=∠FPN+∠MPF=90°, 可知∠EPM=∠FPN, ∴△PFN∽△PEM, ∴  , ,又∵Rt△AEP和Rt△PFC中:∠A=30°,∠C=60°, ∴PF=  PC,PE= PC,PE=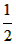 PA, PA,∴  ,∵PC= ,∵PC= PA, PA,∴  。 。 |


科目:初中数学 来源: 题型:044
如图1,小明将一张矩形纸片沿对角线剪开,得到两张三角形纸片(如图2),量得他们的斜边长为10cm,较小锐角为30°,再将这两张三角纸片摆成如图3的形状,但点B、C、F、D在同一条直线上,且点C与点F重合(在图3至图6中统一用F表示)
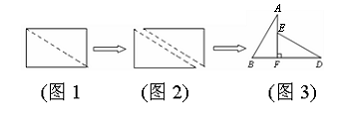
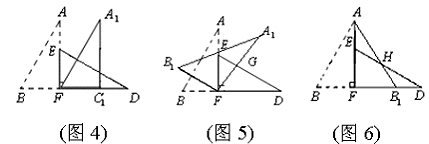
小明在对这两张三角形纸片进行如下操作时遇到了三个问题,请你帮助解决.
(1)
将图3中的△ABF沿BD向右平移到图4的位置,使点B与点F 重合,请你求出平移的距离;(2)
将图3中的△ABF绕点F顺时针方向旋转30°到图5的位置,A1F交DE于点G,请你求出线段FG的长度;(3)
将图3中的△ABF沿直线AF翻折到图6的位置,AB1交DE于点H,请证明:AH﹦DH查看答案和解析>>
科目:初中数学 来源:2007年浙江省义乌市初中毕业、升学统一考试数学试卷 题型:044
如图1,小明将一张矩形纸片沿对角线剪开,得到两张三角形纸片(如图2),量得他们的斜边长为10 cm,较小锐角为30°,再将这两张三角纸片摆成如图3的形状,但点B、C、F、D在同一条直线上,且点C与点F重合(在图3至图6中统一用F表示)小明在对这两张三角形纸片进行如下操作时遇到了三个问题,请你帮助解决.

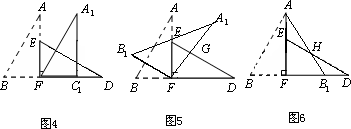
(1)将图3中的△ABF沿BD向右平移到图4的位置,使点B与点F重合,请你求出平移的距离;
(2)将图3中的△ABF绕点F顺时针方向旋转30°到图5的位置,A1F交DE于点G,请你求出线段FG的长度;
(3)将图3中的△ABF沿直线AF翻折到图6的位置,AB1交DE于点H,请证明:AH﹦DH
查看答案和解析>>
科目:初中数学 来源:2007年浙江省初中毕业升学统一考试、数学试题 题型:059
如图1,小明将一张矩形纸片沿对角线剪开,得到两张三角形纸片(如图2),量得他们的斜边长为10 cm,较小锐角为30°,再将这两张三角纸片摆成如图3的形状,但点B、C、F、D在同一条直线上,且点C与点F重合(在图3至图6中统一用F表示)
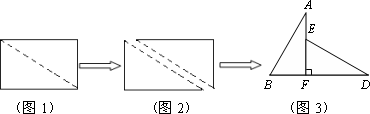
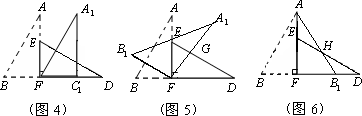
小明在对这两张三角形纸片进行如下操作时遇到了三个问题,请你帮助解决.
(1)将图3中的△ABF沿BD向右平移到图4的位置,使点B与点F重合,请你求出平移的距离;
(2)将图3中的△ABF绕点F顺时针方向旋转30°到图5的位置,A1F交DE于点G,请你求出线段FG的长度;
(3)将图3中的△ABF沿直线AF翻折到图6的位置,AB1交DE于点H,请证明:AH﹦DH
查看答案和解析>>
科目:初中数学 来源:2012届吉林省初三上学期第二次月考数学试卷 题型:解答题
在图1至图3中,点B是线段AC的中点,点D是线段CE的中点.四边形BCGF和CDHN都是正方形.AE的中点是M.

1.如图1,点E在AC的延长线上,点N与点G重合时,点M与点C重合,
求证:FM = MH,FM⊥MH
2.将图-1中的CE绕点C顺时针旋转一个锐角,得到图2,
求证:△FMH是等腰直角三角形
3.将图2中的CE缩短到图3的情况,△FMH还是等腰直角三角形吗?(不必
说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
如图(1),小明将一张矩形纸片沿对角线剪开,得到两张三角形纸片(如图(2)),量得他们的斜边长为10cm,较小锐角为30°,再将这两张三角纸片摆成如图(3)的形状,但点B、C、F、D在同一条直线上,且点C与点F重合(在图(3)至图(6)中统一用F表示)
小明在对这两张三角形纸片进行如下操作时遇到了三个问题,请你帮助解决。
(1)将图(3)中△ABF沿BD向右平移到图(4)的位置,使点B与点F重合,请你求出平移的距离;
(2)将图(3)中△ABF绕点F顺时针方向旋转30°到图(5)的位置,A1F交DE于点G,请你求出线段FG的长度;
(3)将图(3)中的△ABF沿直线AF翻折到图(6)的位置,AB1交DE丁点H,请证明:AH=DH。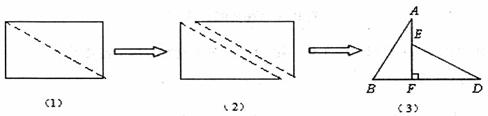
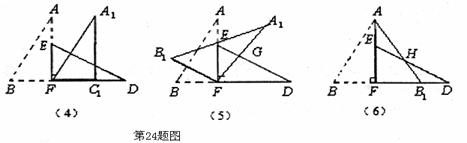
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com